题目内容
3.设随机变量X的分布列为P(X=k)=$\frac{c}{k(k+1)}$(c为常数),k=1,2,3,4,则P(1.5<k<3.5)=$\frac{5}{16}$.分析 随机变量X的所有可能取值为1,2,3,4,根据它们的概率之和为1,求出c的值,进一步求出P(1.5<k<3.5)的值.
解答 解:由随机变量X的分布列为P(X=k)=$\frac{c}{k(k+1)}$(c为常数),k=1,2,3,4,
得$\frac{c}{1×(1+1)}+\frac{c}{2×(2+1)}+\frac{c}{3×(3+1)}$$+\frac{c}{4×(4+1)}=1$,
解c=$\frac{5}{4}$.
∴P(1.5<k<3.5)=P(X=2)+P(X=3)=$\frac{5}{24}+\frac{5}{48}=\frac{5}{16}$.
故答案为:$\frac{5}{16}$.
点评 本题考查了离散型随机变量的期望与方差,解决随机变量的分布列问题,一定要注意分布列的特点,各个概率值在[0,1]之间,概率和为1,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若以C的焦点F为圆心a为半径的圆,截双曲线的渐近线所得弦长为b,则此双曲线的离心率是( )
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
12.在△ABC中,a=3$\sqrt{3}$,b=2,cosC=$-\frac{{\sqrt{3}}}{2}$,则c等于( )
| A. | 13 | B. | $\sqrt{13}$ | C. | 7 | D. | 9 |
2.某种设备购入之后从第二年开始每年都需要返厂进行硬件维修和软件升级,已知其使用年份x1(年)与所支出的返厂费用y1(万元)的数据资料算得如表结果:
(1)求所支出的返厂费用y对使用年份x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)当使用年份为9年时,试估计返厂所需要支出的费用是多少?
(在线性回归方程$\widehat{y}$=$\widehat{b}$x$\widehat{a}$中,$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}{y}_{1}-n\widehat{x}\widehat{y}}{\underset{\stackrel{n}{∑}}{n-1}{x}_{1}^{2}-n\widehat{x}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\widehat{x}$,$\widehat{y}$为样本平均值)
| x1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 2.5 | 4 | 5 | 6 | 7.5 |
(2)当使用年份为9年时,试估计返厂所需要支出的费用是多少?
(在线性回归方程$\widehat{y}$=$\widehat{b}$x$\widehat{a}$中,$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}{y}_{1}-n\widehat{x}\widehat{y}}{\underset{\stackrel{n}{∑}}{n-1}{x}_{1}^{2}-n\widehat{x}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\widehat{x}$,$\widehat{y}$为样本平均值)
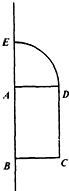 如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )
如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )