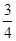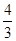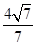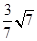题目内容
已知 为椭圆
为椭圆 的左、右焦点,若
的左、右焦点,若 为椭圆上一点,且△
为椭圆上一点,且△ 的内切圆的周长等于
的内切圆的周长等于 ,则满足条件的点
,则满足条件的点 有
有
 为椭圆
为椭圆 的左、右焦点,若
的左、右焦点,若 为椭圆上一点,且△
为椭圆上一点,且△ 的内切圆的周长等于
的内切圆的周长等于 ,则满足条件的点
,则满足条件的点 有
有| A.0个 | B.1个 | C.2个 | D.4个 |
C
解:设△MF1F2的内切圆的内切圆的半径等于r,则由题意可得 2πr=3π,∴r=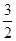 .
.
由椭圆的定义可得 MF1 +MF2=2a=10,又 2c=6,
∴△ 的面积等于
的面积等于 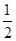 ( MF1 +MF2+2c )r=8r=12.
( MF1 +MF2+2c )r=8r=12.
又△ 的面积等于
的面积等于 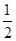 2c yM=12,∴yM=4,故 M是椭圆的短轴顶点,故满足条件的点M有2个,
2c yM=12,∴yM=4,故 M是椭圆的短轴顶点,故满足条件的点M有2个,
故选 C.
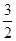 .
.由椭圆的定义可得 MF1 +MF2=2a=10,又 2c=6,
∴△
 的面积等于
的面积等于 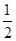 ( MF1 +MF2+2c )r=8r=12.
( MF1 +MF2+2c )r=8r=12.又△
 的面积等于
的面积等于 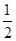 2c yM=12,∴yM=4,故 M是椭圆的短轴顶点,故满足条件的点M有2个,
2c yM=12,∴yM=4,故 M是椭圆的短轴顶点,故满足条件的点M有2个,故选 C.

练习册系列答案
相关题目
 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心, 相切.
相切. ,
, 、
、 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆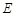 ,求直线
,求直线 与
与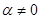 的直线
的直线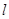 过椭圆
过椭圆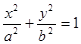
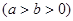 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则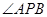 为 ( )
为 ( ) 轴上,经过点
轴上,经过点 ,离心率
,离心率 .
.
 、
、 ,点
,点 为直线
为直线 上任意一点(点
上任意一点(点 交椭圆于
交椭圆于 点,连结
点,连结 并延长交椭圆于
并延长交椭圆于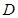 点,试问:是否存在
点,试问:是否存在 ,使得
,使得 成立,若存在,求出
成立,若存在,求出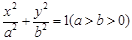 ,过右焦点且不与
,过右焦点且不与 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于 ,
,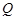 两点,若在椭圆的右准线上存在点
两点,若在椭圆的右准线上存在点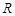 ,使
,使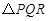 为正三角形,则椭圆的离心率的取值范围是 .
为正三角形,则椭圆的离心率的取值范围是 . 是椭圆
是椭圆 上的一点,若
上的一点,若 ,则点
,则点 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为

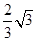

 和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 点,若直线
点,若直线 恰与圆
恰与圆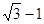



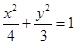 上的一点,
上的一点,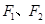 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若 的内切圆的半径为
的内切圆的半径为 ,则
,则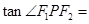 ( )
( )