题目内容
椭圆中心在原点，焦点在坐标轴上，有两顶点的坐标是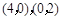
，椭圆的方程是
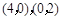，椭圆的方程是A． 或  | B． |
| C． | D． |
C
解：因为椭圆中心在原点，焦点在坐标轴上，有两顶点的坐标是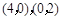，则可知a=4,b=2,则根据焦点在x轴上，则椭圆的方程是，选C
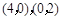，则可知a=4,b=2,则根据焦点在x轴上，则椭圆的方程是，选C
练习册系列答案
相关题目
题目内容
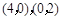，椭圆的方程是| A．或 | B． |
| C． | D． |
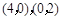，则可知a=4,b=2,则根据焦点在x轴上，则椭圆的方程是，选C
：
的离心率为
，以原点为圆心，
相切．
，
、
是椭圆
轴对称的任意两个不同的点，连结
交椭圆
，求直线
与
与双曲线
的左右两支分别交于
、
两点，与双曲线
的右准线相交于
点，
为右焦点，若
，又
，则实数
的值为
的直线
过椭圆
的右焦点Ｆ交椭圆于Ａ、Ｂ两点，Ｐ为右准线上任意一点，则
为 （ ）
的焦点为顶点，以椭圆的顶点为焦点的双曲线的方程． 
中，
，动点P的轨迹为曲线E，曲线E过点C且满足|PA|+|PB|为常数。
平分？若存在，求出L的斜率的取值范围；若不存在说明理由。
的左顶点为A1，右焦点为F2，点P为该椭圆上一动点，则当
取最小值时，
的值为（ ）
的焦点与椭圆
的焦点重合，则此双曲线的离心率为
和
为椭圆的两个焦点，以
为圆心作圆，已知圆
点，若直线
恰与圆
