题目内容
12.在复平面上,复数z=a+bi(a,b∈R)与复数i(i-2)关于实轴对称,则a+b的值为( )| A. | 1 | B. | -3 | C. | 3 | D. | 2 |
分析 先化简i(i-2)=-1-2i,利用关于实轴对称可得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,进而可得结论.
解答 解:∵z=a+bi(a,b∈R)与复数i(i-2)=-1-2i关于实轴对称,
∴$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,∴a+b=2-1=1,
故选:A.
点评 本题考查复数的运算,注意解题方法的积累,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
20.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{b}$=1(a>b>0)的左顶点A且斜率为k的直线交椭圆于另一个点B,且点B在x轴上的射影恰好为右焦点F,若0<k<$\frac{1}{3}$,则椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
7.已知向量$\overrightarrow{a}=({e}^{x},1)$,向量$\overrightarrow{b}=(1,x-1)$,设函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,则函数f(x)的零点个数为( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
17.已知a>b>0,则下列不等式一定成立的是( )
| A. | ${(\frac{1}{4})^a}<{(\frac{1}{3})^b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ln(a-b)>0 | D. | 3a-b<1 |
4.若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
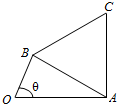 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.