题目内容
16.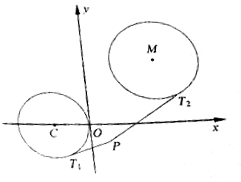 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
分析 设P(x,y),利用$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$,可得$\frac{(x+4)^{2}+{y}^{2}-16}{{x}^{2}+{y}^{2}-2ax-2(8-a)y+4a+22}$=$\frac{1}{4}$,从$\left\{\begin{array}{l}{2x-2y-4=0}\\{3{x}^{2}+3{y}^{2}+32x+16y-22=0}\end{array}\right.$,即可得出结论.
解答 解:圆C:(x+4)2+y2=16的圆心为(-4,0),半径为4,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0的圆心为(a,8-a),半径为$\sqrt{2{a}^{2}-20a+42}$
设P(x,y),则
因为$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$,
所以$\frac{(x+4)^{2}+{y}^{2}-16}{{x}^{2}+{y}^{2}-2ax-2(8-a)y+4a+22}$=$\frac{1}{4}$,
所以3x2+3y2+(32+2a)x+2(8-a)y-4a-22=0,
所以a(2x-2y-4)+(3x2+3y2+32x+16y-22)=0,
所以$\left\{\begin{array}{l}{2x-2y-4=0}\\{3{x}^{2}+3{y}^{2}+32x+16y-22=0}\end{array}\right.$,
可得y2+10y+9=0,∴y=-1或-9,
∴P(1,-1)或P(-7,-9).
点评 本题考查圆与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
6.已知集合$A=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,B={x|1≤3x≤9},则A∩B=( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
7.已知向量$\overrightarrow{a}=({e}^{x},1)$,向量$\overrightarrow{b}=(1,x-1)$,设函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,则函数f(x)的零点个数为( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
4.若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线l过焦点F,且斜率为k,则直线l与双曲线C的左、右两支都相交的充要条件是( )
| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
9.已知区域D:$\left\{\begin{array}{l}y≥2\\ x+y-2≥0\\ x-y-1≤0.\end{array}\right.$若圆C:(x-a)2+(y-2)2=2与区域D有公共点,则实数a的取值范围是( )
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
10.“a>3”是“函数f(x)=ax+3在(-1,2)上存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |