题目内容
15.已知x,y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}\right.$,则|x+y+1|的最大值为6.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求解即可.
解答 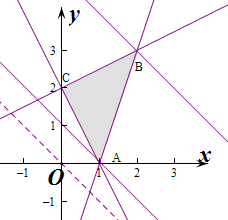 解:作出不等式组对应的平面区域如图:(阴影部分ABC).
解:作出不等式组对应的平面区域如图:(阴影部分ABC).
设z=x+y+1得y=-x+z-1,平移直线y=-x+z-1,
由图象可知当直线y=-x+z-1经过点A(1,0)时,
直线y=-x+z-1的截距最小,此时z最小.
此时z=1+1=2,
当直线经过点B时,直线截距最大,
由$\left\{\begin{array}{l}{x-2y+4=0}\\{3x-y-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即B(2,3),
代入目标函数z=x+y+1得z=2+3+1=6.
即2≤z≤6,
则2≤|x+y+1|≤6,
故|x+y+1|的最大值为6.
故答案为:6.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
6.已知集合$A=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,B={x|1≤3x≤9},则A∩B=( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
20.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{b}$=1(a>b>0)的左顶点A且斜率为k的直线交椭圆于另一个点B,且点B在x轴上的射影恰好为右焦点F,若0<k<$\frac{1}{3}$,则椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
7.已知向量$\overrightarrow{a}=({e}^{x},1)$,向量$\overrightarrow{b}=(1,x-1)$,设函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,则函数f(x)的零点个数为( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
4.若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.已知区域D:$\left\{\begin{array}{l}y≥2\\ x+y-2≥0\\ x-y-1≤0.\end{array}\right.$若圆C:(x-a)2+(y-2)2=2与区域D有公共点,则实数a的取值范围是( )
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
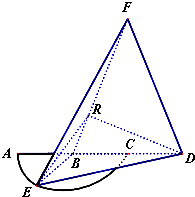 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.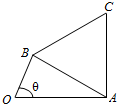 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.