题目内容
(本题14分)函数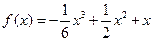 ,
,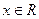 .
.
(Ⅰ)求证:函数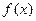 的图象关于点
的图象关于点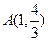 中心对称,并求
中心对称,并求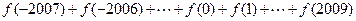 的值.
的值.
(Ⅱ)设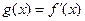 ,
,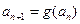 ,
,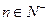 ,且
,且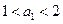 ,
,
求证:(ⅰ)当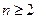 时,
时,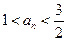 ;(ⅱ)
;(ⅱ)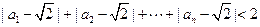 .
.
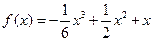 ,
,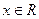 .
.(Ⅰ)求证:函数
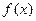 的图象关于点
的图象关于点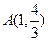 中心对称,并求
中心对称,并求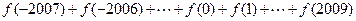 的值.
的值.(Ⅱ)设
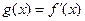 ,
,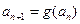 ,
,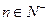 ,且
,且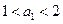 ,
,求证:(ⅰ)当
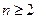 时,
时,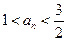 ;(ⅱ)
;(ⅱ)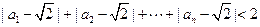 .
.(Ⅰ) 5356 (Ⅱ) 见解析
:(Ⅰ)设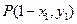 是函数
是函数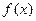 的图象上的任一点,则
的图象上的任一点,则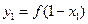 ,
,
又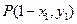 关于
关于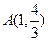 的对称点是
的对称点是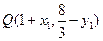 ,(1分)而
,(1分)而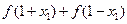
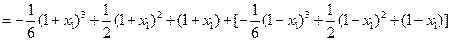
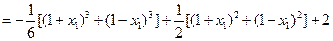
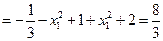 ,即
,即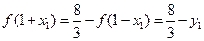 ,(3分)
,(3分)
点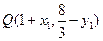 也在函数
也在函数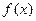 的图象上,故
的图象上,故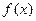 的图象关于点
的图象关于点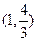 中心对称.(4分)
中心对称.(4分)
 由于
由于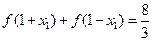 ,
,
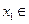 R.
R.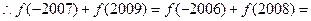 ……
……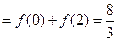 ,
,
又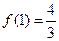 .
.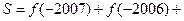 ……
……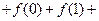 ……
……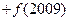 ,
,
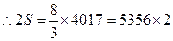 ,
,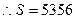 .
.
故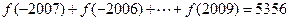 . (6分)
. (6分)
(Ⅱ)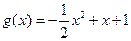 .(ⅰ)下面用数学归纳法证明:
.(ⅰ)下面用数学归纳法证明:
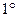 当
当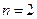 时,
时,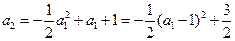
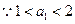
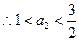 .
.
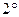 假设
假设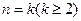 时,
时,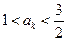 则
则 ,又
,又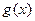 在
在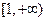 上单调递减,
上单调递减,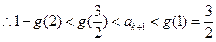 ,这说明
,这说明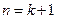 时,命题也成立.
时,命题也成立.
由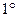
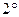 可知
可知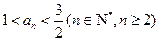 . (10分)
. (10分)
(ⅱ)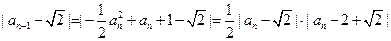 ,
,
由于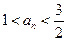 ,
,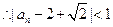 ,
,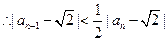 ,
,
于是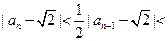 ……
……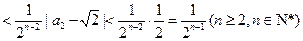 .
.
(12分)
所以,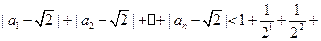 ……
……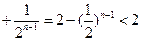 .(14分)
.(14分)
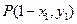 是函数
是函数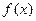 的图象上的任一点,则
的图象上的任一点,则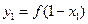 ,
,又
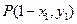 关于
关于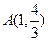 的对称点是
的对称点是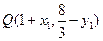 ,(1分)而
,(1分)而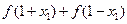
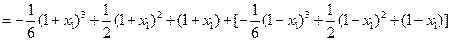
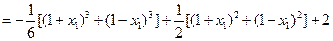
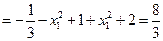 ,即
,即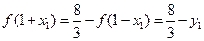 ,(3分)
,(3分)点
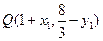 也在函数
也在函数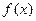 的图象上,故
的图象上,故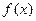 的图象关于点
的图象关于点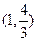 中心对称.(4分)
中心对称.(4分) 由于
由于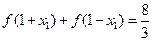 ,
,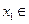 R.
R.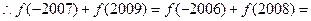 ……
……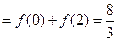 ,
,又
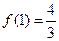 .
.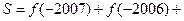 ……
……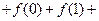 ……
……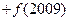 ,
,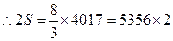 ,
,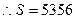 .
.故
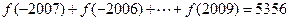 . (6分)
. (6分)(Ⅱ)
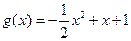 .(ⅰ)下面用数学归纳法证明:
.(ⅰ)下面用数学归纳法证明: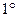 当
当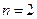 时,
时,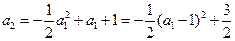
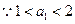
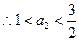 .
.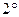 假设
假设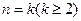 时,
时,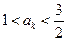 则
则 ,又
,又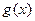 在
在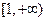 上单调递减,
上单调递减,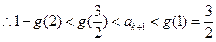 ,这说明
,这说明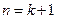 时,命题也成立.
时,命题也成立.由
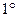
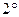 可知
可知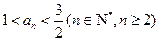 . (10分)
. (10分)(ⅱ)
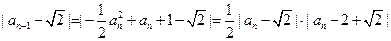 ,
,由于
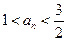 ,
,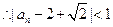 ,
,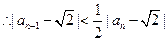 ,
,于是
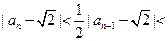 ……
……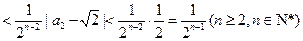 .
.(12分)
所以,
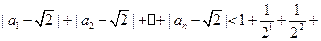 ……
……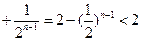 .(14分)
.(14分)
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
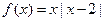 (1)画出函数的图像,写出
(1)画出函数的图像,写出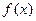 的单调区间;
的单调区间;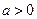 ,求
,求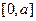 上的最大值
上的最大值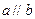 ,求实数
,求实数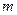 的值;
的值;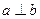 ,求实数
,求实数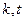 使得
使得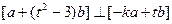 ,试求
,试求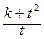 的最小值.
的最小值.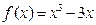 在
在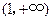 上的单调性并加以证明.
上的单调性并加以证明.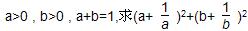 的最小值。
的最小值。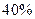 出售,根据市场调查,原价每降低
出售,根据市场调查,原价每降低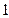 个百分点,月销售件数将增加
个百分点,月销售件数将增加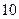 个百分点,为使月毛利润(=月销售总额-月成本总额)比原来增加幅度不小于
个百分点,为使月毛利润(=月销售总额-月成本总额)比原来增加幅度不小于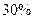 ,问降价至多多少个百分点?
,问降价至多多少个百分点?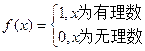 ,
,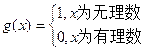 ,则
,则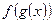 =_____________。
=_____________。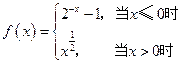 若
若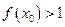 ,求
,求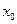 的取值范围 .
的取值范围 .