题目内容
已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若在区间[-1,1]内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________.
(-3,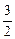 )
)
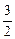 )
) 只需f(1)=-2p2-3p+9>0或f(-1)=-2p2+p+1>0即-3<p<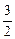 或-
或-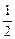 <p<1.∴p∈(-3,
<p<1.∴p∈(-3,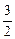 ).
).
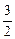 或-
或-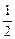 <p<1.∴p∈(-3,
<p<1.∴p∈(-3,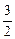 ).
).
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
题目内容
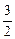 )
)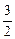 或-
或-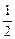 <p<1.∴p∈(-3,
<p<1.∴p∈(-3,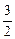 ).
).
 金钥匙试卷系列答案
金钥匙试卷系列答案