题目内容
已知: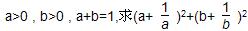 的最小值。
的最小值。
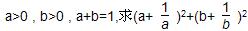 的最小值。
的最小值。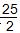
错解(a+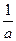 )2+(b+
)2+(b+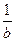 )2=a2+b2+
)2=a2+b2+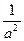 +
+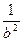 +4≥2ab+
+4≥2ab+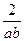 +4≥4
+4≥4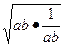 +4=8,
+4=8,
∴(a+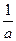 )2+(b+
)2+(b+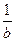 )2的最小值是8.
)2的最小值是8.
分析上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b=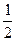 ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=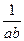 ,显然,这两个条件是不能同时成立的。因此,8不是最小值。
,显然,这两个条件是不能同时成立的。因此,8不是最小值。
事实上,原式= a2+b2+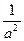 +
+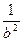 +4="(" a2+b2)+(
+4="(" a2+b2)+(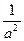 +
+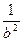 )+4=[(a+b)2-2ab]+[(
)+4=[(a+b)2-2ab]+[(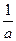 +
+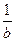 )2-
)2-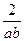 ]+4= (1-2ab)(1+
]+4= (1-2ab)(1+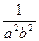 )+4,
)+4,
由ab≤( )2=
)2=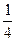 得:1-2ab≥1-
得:1-2ab≥1-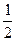 =
=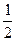 , 且
, 且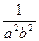 ≥16,1+
≥16,1+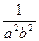 ≥17,
≥17,
∴原式≥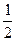 ×17+4=
×17+4=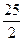 (当且仅当a=b=
(当且仅当a=b=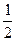 时,等号成立),
时,等号成立),
∴(a +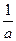 )2 + (b +
)2 + (b + 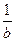 )2的最小值是
)2的最小值是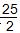 。
。
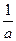 )2+(b+
)2+(b+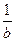 )2=a2+b2+
)2=a2+b2+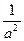 +
+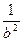 +4≥2ab+
+4≥2ab+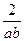 +4≥4
+4≥4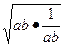 +4=8,
+4=8,∴(a+
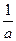 )2+(b+
)2+(b+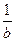 )2的最小值是8.
)2的最小值是8.分析上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b=
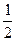 ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=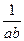 ,显然,这两个条件是不能同时成立的。因此,8不是最小值。
,显然,这两个条件是不能同时成立的。因此,8不是最小值。事实上,原式= a2+b2+
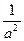 +
+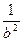 +4="(" a2+b2)+(
+4="(" a2+b2)+(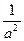 +
+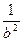 )+4=[(a+b)2-2ab]+[(
)+4=[(a+b)2-2ab]+[(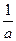 +
+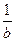 )2-
)2-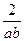 ]+4= (1-2ab)(1+
]+4= (1-2ab)(1+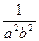 )+4,
)+4,由ab≤(
 )2=
)2=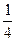 得:1-2ab≥1-
得:1-2ab≥1-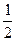 =
=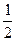 , 且
, 且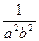 ≥16,1+
≥16,1+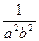 ≥17,
≥17,∴原式≥
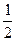 ×17+4=
×17+4=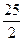 (当且仅当a=b=
(当且仅当a=b=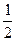 时,等号成立),
时,等号成立),∴(a +
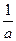 )2 + (b +
)2 + (b + 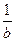 )2的最小值是
)2的最小值是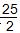 。
。
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
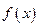 和
和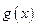 在
在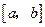 上的图象是连续不断的一条曲线,而且
上的图象是连续不断的一条曲线,而且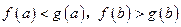 .证明:在
.证明:在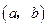 上至少存在一个
上至少存在一个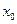 ,使
,使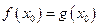 .
. ,g(x)=
,g(x)= .
.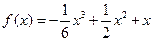 ,
,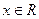 .
.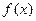 的图象关于点
的图象关于点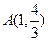 中心对称,并求
中心对称,并求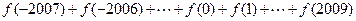 的值.
的值.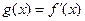 ,
,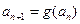 ,
,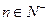 ,且
,且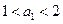 ,
,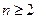 时,
时,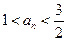 ;(ⅱ)
;(ⅱ)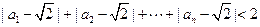 .
.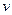 (单位:cm
(单位:cm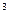 /s)与管道半径
/s)与管道半径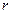 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比. (dB)由公式
(dB)由公式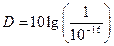 给出,其中
给出,其中 为声强(W/cm
为声强(W/cm ).声强小于
).声强小于 W/cm
W/cm 时,人听不见声音.求:
时,人听不见声音.求: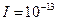 W/cm
W/cm W/cm
W/cm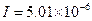 W/cm
W/cm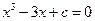 在
在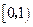 上至多有一实根.
上至多有一实根.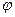 (t),求
(t),求
