题目内容
4.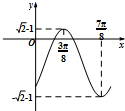 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
分析 根据函数的图象,先求出函数的解析式,结合三角形的面积公式进行求解即可.
解答 解:由函数的图象可知函数的最大值为a-b=$\sqrt{2}$-1,最小值为-a-b=-$\sqrt{2}$-1,
解得a=$\sqrt{2}$,b=1,
$\frac{T}{2}$=$\frac{7π}{8}-\frac{3π}{8}$=$\frac{4π}{8}=\frac{π}{2}$,
即函数的周期T=π,
即 $\frac{2π}{ω}$=π,
即ω=2,
故f(x)=$\sqrt{2}$sin(2x+θ)-1,
∵f($\frac{3π}{8}$)=$\sqrt{2}$sin(2×$\frac{3π}{8}$+θ)-1=$\sqrt{2}-1$,
∴sin($\frac{3π}{4}$+θ)=1,
即$\frac{3π}{4}$+θ=2kπ+$\frac{π}{2}$,
即θ=2kπ-$\frac{π}{4}$,k∈Z.
∵|θ|<$\frac{π}{2}$,
∴k=0时,θ=-$\frac{π}{4}$,
故f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)-1,
∵$cosC=f(\frac{C}{2})+1$,
∴cosC=$\sqrt{2}$sin(C-$\frac{π}{4}$)-1+1=sinC-cosC,
即sinC=2cosC,
平方得sin2C=4cos2C,
5sin2C=4,解得sinC=$\frac{2\sqrt{5}}{5}$,
则△ABC的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}×\sqrt{2}×1×\frac{2\sqrt{5}}{5}$=$\frac{{\sqrt{10}}}{5}$,
故答案为:$\frac{{\sqrt{10}}}{5}$.
点评 本题主要考查三角函数解析式的求解,以及三角形面积公式的计算,根据图象求出三角函数的解析式是解决本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 对任意x≥2,都有x2<4 | B. | 对x<2,都有x2≥4 | ||
| C. | 存在x≥2,使x2<4 | D. | 存在x<2,使x2≥4 |
| A. | {(1,1)} | B. | {(-1,1),(1,1)} | C. | $[{\frac{1}{2},+∞})$ | D. | $[{\frac{{\sqrt{2}}}{2},+∞})$ |
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | $\frac{1}{4030}$ | D. | -$\frac{1}{4030}$ |