题目内容
15.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反,且|$\overrightarrow{a}$|=3与|$\overrightarrow{b}$|=4,求|2$\overrightarrow{a}$-$\overrightarrow{b}$|的值.分析 利用|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(2\overrightarrow{a}-\overrightarrow{b})^{2}}$计算即可.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反,
∴cos<$\overrightarrow a$,$\overrightarrow b$>=cosπ=-1,
又∵|$\overrightarrow{a}$|=3、|$\overrightarrow{b}$|=4,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos<$\overrightarrow a$,$\overrightarrow b$>=-12,
∴$(2\overrightarrow{a}-\overrightarrow{b})^{2}$=4${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=36+48+16=100,
∴|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(2\overrightarrow{a}-\overrightarrow{b})^{2}}$=10.
点评 本题考查平面向量数量积的性质及其计算,注意解题方法的积累,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
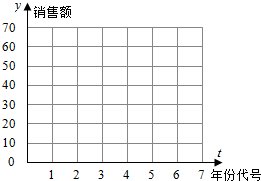
7.我市某大型企业2008年至2014年销售额y(单位:亿元)的数据如下表所示:
(1)在下表中,画出年份代号与销售额的散点图;
(2)求y关于t的线性回归方程,相关数据保留两位小数;
(3)利用所求回归方程,说出2008年至2014年该大型企业销售额的变化情况,并预测该企业2015年的销售额,相关数据保留两位小数.
附:回归直线的斜率的最小二乘法估计公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$.
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |

(2)求y关于t的线性回归方程,相关数据保留两位小数;
(3)利用所求回归方程,说出2008年至2014年该大型企业销售额的变化情况,并预测该企业2015年的销售额,相关数据保留两位小数.
附:回归直线的斜率的最小二乘法估计公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$.
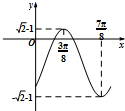 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.