题目内容

14．已知点A（1，2）、B（-2，3），在x轴上找一点P，使|PA|+|PB|有最小值．

分析 设点A（1，2）关于x轴的对称点为A′（1，-2），则点P应是直线A′B和x轴的交点．用两点式直线A′B的方程，可得点P的坐标．

解答 解：设点A（1，2）关于x轴的对称点为A′（1，-2），则|PA|+|PB|=|PA′|+|PB|，
故当点P是直线A′B和x轴的交点时，|PA|+|PB|最小．
由于直线A′B的方程为$\frac{y+2}{3+2}$=$\frac{x-1}{-2-1}$．
令y=0，求得x=$\frac{1}{5}$，可得点P（$\frac{1}{5}$，0）．

点评 本题主要考查点关于直线对称的性质，用两点式求直线的方程，属于基础题．

练习册系列答案
相关题目
4．已知函数f（x）=4cos（$\frac{πx}{2}$+$\frac{π}{3}$），如果对于任意x∈R都有f（x1）≤f（x）≤f（x2）成立，则|x1-x2|的最小值是2．
5．已知函数f（x）=$\frac{x+3}{{x}^{2}+1}$，g（x）=x-ln（x-p）．
（Ⅰ）求函数f（x）的图象在点（$\frac{1}{3}$，f（$\frac{1}{3}$））处的切线方程；
（Ⅱ）判断函数g（x）的零点个数，并说明理由；
（Ⅲ）已知数列{an}满足：0＜an≤3，n∈N*，且3（a1+a2+…+a2015）=2015．若不等式f（a1）+f（a2）+..+f（a2015）≤g（x）在x∈（p，+∞）时恒成立，求实数p的最小值．
2．为了保护环境，某市设立了若干个自行车自动租赁点，规定租车时间不超过一小时不收费，一小时以上不超过两小时收费一元，两小时以上，不超过三小时收费两元（不足一小时，按一小时计），甲、乙两人各租车一辆，甲、乙租车时间不超过一小时的概率为$\frac{1}{2}$、$\frac{1}{4}$，一小时以上，不超过两小时的概率为$\frac{1}{4}$、$\frac{1}{2}$，且两人租车时间都不会超过三小时（甲、乙两人租车时间相互独立）．
（1）求甲、乙两人所付租车费相等的概率；
（2）设两人租车费用之和为ξ，求ξ的分布列及数学期望．
9．设数列{an}的前n项和为Sn，满足Sn=$\frac{4}{3}$an-$\frac{1}{3}×$2n+1+$\frac{2}{3}$，n∈N*．
（Ⅰ）求证数列{an+2n}是等比数列，并求数列{an}的通项an；
（Ⅱ）设T（n）=$\frac{{2}^{n}}{{S}_{n}}$，n∈N*，证明：$\sum_{i=1}^{n}$T（i）＜$\frac{3}{2}$；
（Ⅲ）设R（n）=$\sum_{i=1}^{n}$$\frac{1}{i}$，n≥2，证明：$\frac{n}{2}$＜R（$\frac{{a}_{n}}{{2}^{n}}$）＜n．
19．已知向量$\overrightarrow{m}$=（$\sqrt{3}$，sinθ），$\overrightarrow{n}$=（1，cosθ），θ∈（0，$\frac{π}{2}$），$\overrightarrow{m}$与$\overrightarrow{n}$共线．
（Ⅰ）求θ的值；
（Ⅱ）求函数f（x）=sinx+sin（x-θ）在区间上[0，$\frac{5π}{6}$]的最大值和最小值．
6．已知函数f（x）满足：x≥4，则f（x）=2x；当x＜4时f（x）=f（x+1），则f（2+log${\;}_{\frac{1}{2}}$3）=$\frac{64}{3}$．
3．在△ABC中，若角A为锐角，且$\overrightarrow{AB}$=（2，3），$\overrightarrow{AC}$=（3，m），则实数m的取值范围是$（-2，\frac{9}{2}）∪（\frac{9}{2}，+∞）$．
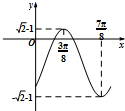4．已知函数f（x）=asin（ωx+θ）-b的部分图象如图，其中ω＞0，|θ|＜$\frac{π}{2}$，a，b分别是△ABC的角A，B所对的边，$cosC=f（\frac{C}{2}）+1$，则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网