题目内容
12．命题“存在x≥2，使x2≥4”的否定是（ ）| A． | 对任意x≥2，都有x2＜4 | B． | 对x＜2，都有x2≥4 | ||
| C． | 存在x≥2，使x2＜4 | D． | 存在x＜2，使x2≥4 |
分析 直接利用特称命题的否定是全称命题，写出结果即可．
解答 解：因为特称命题的否定是全称命题，
所以，命题“存在x≥2，使x2≥4”的否定是：对任意x≥2，都有x2＜4．
故选：A．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
7．我市某大型企业2008年至2014年销售额y（单位：亿元）的数据如下表所示：
（1）在下表中，画出年份代号与销售额的散点图；
（2）求y关于t的线性回归方程，相关数据保留两位小数；
（3）利用所求回归方程，说出2008年至2014年该大型企业销售额的变化情况，并预测该企业2015年的销售额，相关数据保留两位小数．
附：回归直线的斜率的最小二乘法估计公式：b=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$．
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
（2）求y关于t的线性回归方程，相关数据保留两位小数；
（3）利用所求回归方程，说出2008年至2014年该大型企业销售额的变化情况，并预测该企业2015年的销售额，相关数据保留两位小数．
附：回归直线的斜率的最小二乘法估计公式：b=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$．
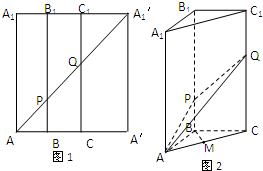如图1，在边长为12的正方形AA′A${\;}_{1}^{′}$A1中，BB1∥CC1∥AA1，且AB=3，且BC=4，AA${\;}_{1}^{′}$分别交BB1，CC1于点P，Q，将该正方形沿BB1，CC1折叠，使得A′A${\;}_{1}^{′}$与AA1重合，构成图2所示的三棱柱ABC-A1B1C1，在图2中：
已知函数f（x）=asin（ωx+θ）-b的部分图象如图，其中ω＞0，|θ|＜$\frac{π}{2}$，a，b分别是△ABC的角A，B所对的边，$cosC=f（\frac{C}{2}）+1$，则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$．