题目内容
14.已知数列{an}中a1=1,an+1-Sn=n+1,n∈N*,{an}的前n项和为Sn.(Ⅰ)证明:数列{an+1}是等比数列;
(Ⅱ)对一切n∈N*,若p(an+1)>3n-1恒成立,求实数p的取值范围.
分析 (I)an+1-Sn=n+1,n∈N*,当n≥2时,an-Sn-1=n,可化为an+1+1=2(an+1).利用等比数列的通项公式即可得出.
(II)由(I)可得:${a}_{n}={2}^{n}-1$,由p(an+1)>3n-1恒成立,可得p>$\frac{3n-1}{{2}^{n}}$,令f(n)=$\frac{3n-1}{{2}^{n}}$,n∈N*.
通过作差研究其单调性即可得出.
解答 (I)证明:∵an+1-Sn=n+1,n∈N*,当n≥2时,an-Sn-1=n,
∴an+1-an-an=1,化为an+1+1=2(an+1).
由a1=1,a2-a1=2,解得a2=3,∴a2+1=2(a1+1),
∴数列{an+1}是等比数列,首项为2,公比为2.
(II)解:由(I)可得:an+1=2n,
∴${a}_{n}={2}^{n}-1$,
由p(an+1)>3n-1恒成立,可得p>$\frac{3n-1}{{2}^{n}}$,
令f(n)=$\frac{3n-1}{{2}^{n}}$,n∈N*.
则f(n+1)-f(n)=$\frac{3(n+1)-1}{{2}^{n+1}}$-$\frac{3n-1}{{2}^{n}}$=$\frac{4-3n}{{3}^{n+1}}$,
当n=1时,由f(n+1)>f(n);当n≥2时,有f(n+1)<f(n),
∴当n=2时,[f(n)]max=$\frac{5}{4}$.
∴$p>\frac{5}{4}$.
即实数p的取值范围是$(\frac{5}{4},+∞)$.
点评 本题考查了等比数列的通项公式、数列的单调性、递推式的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值,若对于任意的x∈[0,3],都有f(x)<c2成立,则实数c的取值范围为( )
| A. | (-1,9) | B. | (-9,1) | C. | (-∞,-1)∪(9,+∞) | D. | (-∞,-9)∪(1,+∞) |
3.下列不等式(组)的解为{x|x<0}的是( )
| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
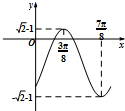 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.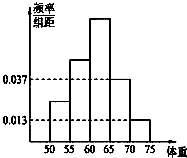 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.