题目内容
9.已知函数f(x)=x-$\frac{1}{x}+\frac{alnx}{2}$(Ⅰ)当a=-1时,求函数f(x)在点A(1,0)处的切线方程;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若函数f(x)有两个极值点x1和x2,设过M(x1,f(x1)),N(x2,f(x2))的直线的斜率为k,求证:k>a+2.
分析 (Ⅰ)求出a=-1时,函数的导数,求得切线的斜率,由点斜式方程即可得到切线方程;
(Ⅱ)求得导数,令g(x)=2x2+ax+2(x>0),对判别式大于0,小于等于0,解不等式即可得到单调区间;
(Ⅲ)求出斜率k,结合分析法证明,即证$ln{x_2}-{x_2}+\frac{1}{x_2}<0$在(1,+∞)上恒成立.令$h(x)=lnx-x+\frac{1}{x}$,x∈(1,+∞),求出导数,运用单调性即可得证.
解答 解:(Ⅰ)当a=-1时,$f(x)=x-\frac{1}{x}-\frac{lnx}{2}$,
则${f^'}(x)=1+\frac{1}{x^2}-\frac{1}{2x}$,∴${f^'}(1)=\frac{3}{2}$,
∴函数f(x)在点A(1,0)处的切线方程$y=\frac{3}{2}({x-1})$,
化简得3x-2y-3=0;
(Ⅱ)${f^'}(x)=1+\frac{1}{x^2}+\frac{a}{2x}=\frac{{2{x^2}+ax+2}}{{2{x^2}}}(x>0)$,
令g(x)=2x2+ax+2(x>0)
①当△=a2-16≤0时,g(x)≥0,2x2>0,
则f′(x)≥0在(0,+∞)恒成立,f(x)在(0,+∞)上单调递增;
②当△=a2-16>0时
(ⅰ)当a>4时,g(x)>0,则f′(x)≥0在(0,+∞)恒成立,
f(x)在(0,+∞)上单调递增;
(ⅱ)当a<-4时,g(x)=0有两根,又g(0)=2>0,
对称轴$x=-\frac{a}{4}>1$,且$0<{x_1}=\frac{{-a-\sqrt{{a^2}-16}}}{4}$,${x_2}=\frac{{-a+\sqrt{{a^2}-16}}}{4}$,
令g(x)>0,解得0<x<x1或x>x2,此时f′(x)>0
令g(x)<0,解得x1<x<x2,此时f′(x)<0.
综上所述:当-4≤a≤4或a>4时,f(x)在(0,+∞)上单调递增;
当a<-4时,f(x)在$({0,\frac{{-a-\sqrt{{a^2}-16}}}{4}})$和$({\frac{{-a+\sqrt{{a^2}-16}}}{4},+∞})$上单调递增,
在$({\frac{{-a-\sqrt{{a^2}-16}}}{4},\frac{{-a+\sqrt{{a^2}-16}}}{4}})$上单调递减.
(Ⅲ)证明:由(Ⅱ)知函数f(x)有两个极值点x1和x2,则a<-4,且x1x2=1,
不妨设x1<x2
又$k=\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$=$\frac{{{x_2}-\frac{1}{x_2}+\frac{a}{2}ln{x_2}-({{x_1}-\frac{1}{x_1}+\frac{a}{2}ln{x_1}})}}{{{x_2}-{x_1}}}$=$1+\frac{1}{{{x_2}•{x_1}}}+\frac{a}{2}\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}$=$2+\frac{a}{2}\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}$.
∴欲证k>a+2,即证$2+\frac{a}{2}\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}>a+2$,∵a<-4,
即证$\frac{{ln{x_2}-ln{x_1}}}{{2({{x_2}-{x_1}})}}<1$即证lnx2-lnx1<2x2-2x1又x1x2=1,${x_1}=\frac{1}{x_2}$,且x2>1,
即证$ln{x_2}-{x_2}+\frac{1}{x_2}<0$在(1,+∞)上恒成立.
令$h(x)=lnx-x+\frac{1}{x}$,x∈(1,+∞)
∴$h'(x)=\frac{1}{x}-\frac{1}{x^2}-1=\frac{{-{x^2}+x-1}}{x^2}$=$\frac{{-{{({x-\frac{1}{2}})}^2}-\frac{3}{4}}}{x^2}<0$,
∴$h(x)=lnx-x+\frac{1}{x}$在(1,+∞)上是递减函数,
∴h(x)<h(1)=0,
∴$ln{x_2}-{x_2}+\frac{1}{x_2}<0$在(1,+∞)上恒成立
∴k>a+2.
点评 本题考查导数的运用:求切线方程和单调区间、极值,同时考查不等式的恒成立思想,注意运用函数的单调性,考查运算能力,属于中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中: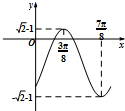 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.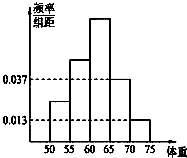 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.