题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知双曲线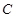 的方程为
的方程为 ,点
,点 和点
和点 (其中
(其中 和
和 均为正数)是双曲线
均为正数)是双曲线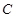 的两条渐近线上的的两个动点,双曲线
的两条渐近线上的的两个动点,双曲线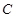 上的点
上的点 满足
满足 (其中
(其中 ).
).
(1)用 的解析式表示
的解析式表示 ;
;
(2)求△ (
( 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.
已知双曲线
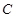 的方程为
的方程为 ,点
,点 和点
和点 (其中
(其中 和
和 均为正数)是双曲线
均为正数)是双曲线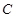 的两条渐近线上的的两个动点,双曲线
的两条渐近线上的的两个动点,双曲线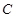 上的点
上的点 满足
满足 (其中
(其中 ).
).(1)用
 的解析式表示
的解析式表示 ;
;(2)求△
 (
( 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.(1)由已知, ,
, (
( ,
, ),设
),设
由 ,
, 得
得 ,故
,故 点的坐标为
点的坐标为 ,…(3分)
,…(3分)
将 点的坐标代入
点的坐标代入 ,化简得,
,化简得,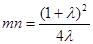 .…………(3分)
.…………(3分)
(2)解法一:设 ,则
,则 ,所以
,所以 .……(1分)
.……(1分)
又 ,
, ,所以
,所以
 ,…………(3分)
,…………(3分)
记 ,
, ,则
,则 在
在 上是减函数,在
上是减函数,在 上是增函数.…………(2分)
上是增函数.…………(2分)
所以,当 时,
时, 取最小值
取最小值 ,当
,当 时,
时, 取最大值
取最大值 .
.
所以△ 面积的取值范围是
面积的取值范围是 .…………(2分)
.…………(2分)
解法二:因为 ,
, (
( ,
, ),所以
),所以

 ,…(4分)
,…(4分)
记 ,
, ,则
,则 在
在 上是减函数,在
上是减函数,在 上是增函数.…………(2分)
上是增函数.…………(2分)
所以,当 时,
时, 取最小值
取最小值 ,当
,当 时,
时, 取最大值
取最大值 .
.
所以△ 面积的取值范围是
面积的取值范围是 .…………(2分)
.…………(2分)
 ,
, (
( ,
, ),设
),设
由
 ,
, 得
得 ,故
,故 点的坐标为
点的坐标为 ,…(3分)
,…(3分)将
 点的坐标代入
点的坐标代入 ,化简得,
,化简得,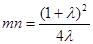 .…………(3分)
.…………(3分)(2)解法一:设
 ,则
,则 ,所以
,所以 .……(1分)
.……(1分)又
 ,
, ,所以
,所以
 ,…………(3分)
,…………(3分)记
 ,
, ,则
,则 在
在 上是减函数,在
上是减函数,在 上是增函数.…………(2分)
上是增函数.…………(2分)所以,当
 时,
时, 取最小值
取最小值 ,当
,当 时,
时, 取最大值
取最大值 .
.所以△
 面积的取值范围是
面积的取值范围是 .…………(2分)
.…………(2分)解法二:因为
 ,
, (
( ,
, ),所以
),所以
 ,…(4分)
,…(4分)记
 ,
, ,则
,则 在
在 上是减函数,在
上是减函数,在 上是增函数.…………(2分)
上是增函数.…………(2分)所以,当
 时,
时, 取最小值
取最小值 ,当
,当 时,
时, 取最大值
取最大值 .
.所以△
 面积的取值范围是
面积的取值范围是 .…………(2分)
.…………(2分)略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

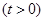 在直线
在直线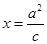 (
(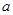 为长半轴,
为长半轴,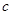 为半焦距)上.
为半焦距)上.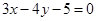 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程; 的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )




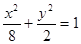 经过点
经过点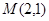 ,
,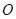 为坐标原点,平行于
为坐标原点,平行于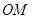 的直线
的直线 在
在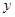 轴上的截距为
轴上的截距为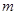
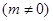 .
.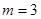 时,判断直线
时,判断直线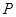 为椭圆上的动点,求点
为椭圆上的动点,求点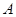 、
、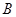 两个不同点时,求证:直线
两个不同点时,求证:直线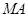 、
、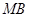 与
与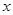 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.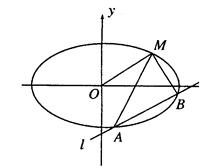
 的左、右焦点为
的左、右焦点为 ,其上顶点为
,其上顶点为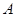 .已知
.已知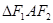 是边长为
是边长为 的正三角形.
的正三角形. 任作一直线
任作一直线 交椭圆C于
交椭圆C于 两
两 若在线段
若在线段 上取一点
上取一点 使得
使得 ,试判断当直线
,试判断当直线 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
 的顶点A、B在椭圆
的顶点A、B在椭圆 ,点
,点 在直线
在直线 上,且
上,且
 ,且斜边AC的长最大时,
,且斜边AC的长最大时, 的离心率为( )
的离心率为( )


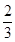
 的离心率为
的离心率为 ,则
,则 的值为_____________.
的值为_____________. ,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.
,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.