��Ŀ����
����Ŀ��ijˮ����ֲ��������һ����ˮ��Ʒ�֣����о����ָ�ˮ��ÿ��IJ���![]() ����λ��
�����![]() ���������������������
���������������������![]() ����������ع�ϵ����������������ָ���ǵ�ֱ�߾��벻����
����������ع�ϵ����������������ָ���ǵ�ֱ�߾��벻����![]() �������ֱ��¼���������Ϊ0��1��2��3��4ʱÿ�����������������£�
�������ֱ��¼���������Ϊ0��1��2��3��4ʱÿ�����������������£�
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
��1���������ˮ��ÿ��IJ���![]() �����������������
�����������������![]() �Ļع鷽�̣�
�Ļع鷽�̣�
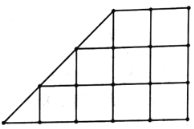
��2������ֲ��������ͼ��ʾ�ij����εؿ��ÿ����㣨����ֱ�ߵĽ��㣩��������һ�����ˮ��������ÿ��С�����ε������Ϊ![]() ���ִ����ֵĸ�ˮ�������ѡȡһ�꣬�Ը��ݣ�1���еĻع鷽�̣�Ԥ�����IJ�����ƽ����.
���ִ����ֵĸ�ˮ�������ѡȡһ�꣬�Ը��ݣ�1���еĻع鷽�̣�Ԥ�����IJ�����ƽ����.
�����ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ�� ��
��![]() .
.

���𰸡���1��![]() ��2��
��2��![]()
��������
��1�������![]() ��
��![]() ���������ϵ��
���������ϵ��![]() ��
��![]() ������ع鷽�̼��ɣ���2������
������ع鷽�̼��ɣ���2������![]() ��ֵ�����
��ֵ�����![]() ��Ԥ��ֵ����ƽ�������ɣ�
��Ԥ��ֵ����ƽ�������ɣ�
�⣺��1��������ã�![]() ��
��
![]() ��
��
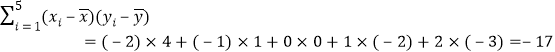 ��
��
![]() ��
��
����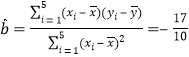 ��
��
![]() ��
��
����![]() .
.
��2���ɻع鷽�̵ã�
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ƽ����Ϊ��![]() .
.
����һ�������ƽ����Ϊ![]() .
.

����Ŀ��ijˮ����ֲ��������һ����ˮ��Ʒ�֣����о����ָ�ˮ��ÿ��IJ���![]() ����λ��
�����![]() ���������������������
���������������������![]() ����������ع�ϵ����������������ָ���ǵ�ֱ�߾��벻����
����������ع�ϵ����������������ָ���ǵ�ֱ�߾��벻����![]() �������ֱ��¼���������Ϊ0��1��2��3��4ʱÿ�����������������£�
�������ֱ��¼���������Ϊ0��1��2��3��4ʱÿ�����������������£�
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
��1���������ˮ��ÿ��IJ���![]() �����������������
�����������������![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��2����һ��ֲ������ֲ����ˮ��500�꣬��ÿ���������������������Ϊ![]() ���ƻ��ջ����ȫ���۳����۸�Ϊ10Ԫ
���ƻ��ջ����ȫ���۳����۸�Ϊ10Ԫ![]() ��������루����=�������۸�����25000Ԫ����
��������루����=�������۸�����25000Ԫ����![]() �����ֵ�Ƕ��٣�
�����ֵ�Ƕ��٣�
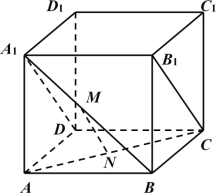
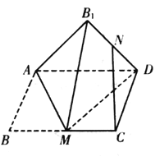
��3������ֲ��������ͼ��ʾ��ֱ�����εؿ��ÿ������㣨ֱ�ߵĽ��㣩��������һ�����ˮ��������ÿ��С�����εı߳���ֱ�������ε�ֱ�DZ߳���Ϊ![]() ����֪�����εؿ��ܱ���������ľӰ�죬�������ֵĸ�ˮ�������ѡȡһ�꣬�Ը��ݣ�1���еĻع鷽�̣�Ԥ�����IJ����ķֲ�������ѧ����.
����֪�����εؿ��ܱ���������ľӰ�죬�������ֵĸ�ˮ�������ѡȡһ�꣬�Ը��ݣ�1���еĻع鷽�̣�Ԥ�����IJ����ķֲ�������ѧ����.
�����ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��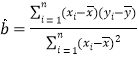 ��
��![]() .
.