题目内容
【题目】已知圆![]() 与直线
与直线![]() 相切,圆心在
相切,圆心在![]() 轴上,且直线
轴上,且直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率乘积为
的斜率乘积为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)设圆![]() 的方程为
的方程为![]() ,则圆心到直线
,则圆心到直线![]() 的距离为
的距离为![]() ,由直线
,由直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,及弦长公式,得关于
,及弦长公式,得关于![]() 的一个方程;再由圆
的一个方程;再由圆![]() 与直线
与直线![]() 相切可得又一关于
相切可得又一关于![]() 的一个方程;联立方程,即可求出
的一个方程;联立方程,即可求出![]() 的值,而得到圆的方程;
的值,而得到圆的方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立直线与圆的方程,消去
,联立直线与圆的方程,消去![]() 得到一个关于
得到一个关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,由韦达定理,可用
,由韦达定理,可用![]() 将直线
将直线![]() 与
与![]() 的斜率乘积为
的斜率乘积为![]() 表示出来,然后由
表示出来,然后由![]() 可求出
可求出![]() 的值,进而就可求出
的值,进而就可求出![]() 的值.
的值.
试题解析:(1)设圆![]() 的方程为
的方程为![]() ,
,
则圆心到直线![]() 的距离为
的距离为![]() ,
,
由直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() 可得
可得
 ,即
,即![]() ,①
,①
由圆![]() 与直线
与直线![]() 相切可得
相切可得 ,即
,即![]() ②,
②,
由①②及![]() 解得
解得![]() ,
,
故圆![]() 的方程为
的方程为![]() ,
,
(2)设直线![]() 的方程为
的方程为![]() ,联立
,联立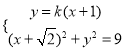 ,
,
得![]() ,
,
则![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
则![]() ,
,
所以![]() ,
,
则 ,
,
故![]()
则![]() ,
,
![]() ,
,
故![]()
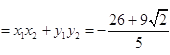

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)该种植基地在如图所示的长方形地块的每个格点(横纵直线的交点)处都种了一株该种水果,其中每个小正方形的面积都为![]() ,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
,![]() .
.