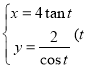题目内容
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
①存在某个位置,使得![]() ;
;
②翻折过程中,![]() 的长是定值;
的长是定值;
③若![]() ,则
,则![]() ;
;
④若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
【答案】②④
【解析】
对于①,取AD中点E,连接EC交MD与F,可得到EN⊥NF,又EN⊥CN,且三线NE,NF,NC共面共点,不可能,
对于②,可得由∠NEC=∠MAB1(定值),NE![]() AB1(定值),AM=EC(定值),由余弦定理可得NC是定值.
AB1(定值),AM=EC(定值),由余弦定理可得NC是定值.
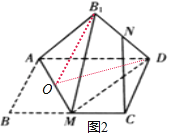
对于③,取AM中点O,连接B1O,DO,易得AM⊥面ODB1,即可得OD⊥AM,从而AD=MD,显然不成立.
对于④:当平面B1AM⊥平面AMD时,三棱锥B1﹣AMD的体积最大,可得球半径为1,表面积是4π.
对于①:如图1,取AD中点E,连接EC交MD与F,则NE∥AB1,NF∥MB1,
如果CN⊥AB1,可得到EN⊥NF,又EN⊥CN,且三线NE,NF,NC共面共点,不可能,故①错.
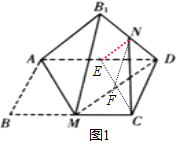
对于②:如图1,可得由∠NEC=∠MAB1(定值),NE![]() AB1(定值),AM=EC(定值),
AB1(定值),AM=EC(定值),
由余弦定理可得NC2=NE2+EC2﹣2NEECcos∠NEC,所以NC是定值,故②正确.
对于③:如图2,取AM中点O,连接B1O,DO,易得AM⊥面ODB1,即可得OD⊥AM,从而AD=MD,显然不成立,可得③不正确.
对于④:当平面B1AM⊥平面AMD时,三棱锥B1﹣AMD的体积最大,易得AD中点H就是三棱锥B1﹣AMD的外接球的球心,球半径为1,表面积是4π.故④正确.
故答案为:②④.

【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)该种植基地在如图所示的长方形地块的每个格点(横纵直线的交点)处都种了一株该种水果,其中每个小正方形的面积都为![]() ,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
,![]() .
.