题目内容
(本题满分12分)已知函数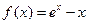 (
(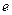 为自然对数的底数).
为自然对数的底数).
(1)求函数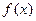 的最小值;
的最小值;
(2)若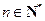 ,证明:
,证明: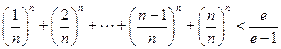 .
.
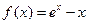 (
(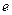 为自然对数的底数).
为自然对数的底数).(1)求函数
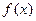 的最小值;
的最小值;(2)若
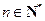 ,证明:
,证明: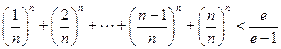 .
.(1)当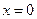 时,
时,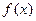 有最小值1
有最小值1
(2)见解析
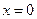 时,
时,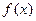 有最小值1
有最小值1(2)见解析
(1)解:∵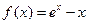 ,∴
,∴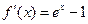 .
.
令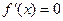 ,得
,得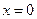 .
.
∴当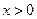 时,
时,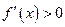 ,当
,当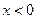 时,
时,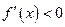 .
.
∴函数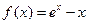 在区间
在区间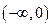 上单调递减,在区间
上单调递减,在区间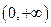 上单调递增.
上单调递增.
∴当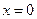 时,
时,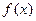 有最小值1.
有最小值1.
(2)证明:由(1)知,对任意实数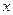 均有
均有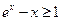 ,即
,即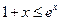 .
.
令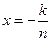 (
(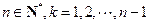 ),则
),则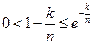 ,
,
∴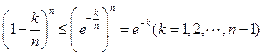 .
.
即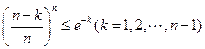 .
.
∵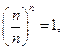
∴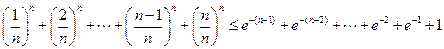 .
.
∵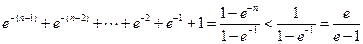 ,
,
∴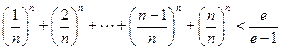 .
.
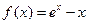 ,∴
,∴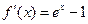 .
.令
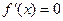 ,得
,得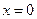 .
.∴当
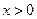 时,
时,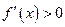 ,当
,当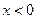 时,
时,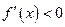 .
.∴函数
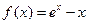 在区间
在区间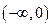 上单调递减,在区间
上单调递减,在区间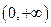 上单调递增.
上单调递增.∴当
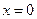 时,
时,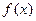 有最小值1.
有最小值1.(2)证明:由(1)知,对任意实数
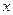 均有
均有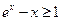 ,即
,即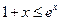 .
.令
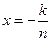 (
(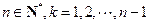 ),则
),则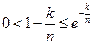 ,
, ∴
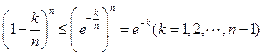 .
. 即
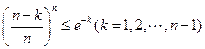 .
. ∵
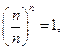
∴
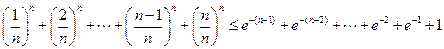 .
.∵
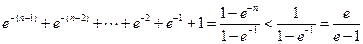 ,
,∴
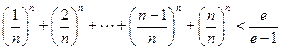 .
.
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
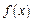 满足
满足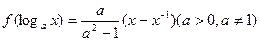
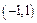 上的单调性(不须证明);
上的单调性(不须证明);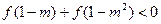 ,求
,求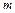 的取值范围;
的取值范围;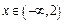 时,关于
时,关于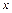 的不等式
的不等式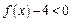 恒成立
恒成立 ,求
,求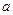 的取值范围.
的取值范围.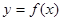 ,则图2中的图象对应的函数在下列四式中只可能是( )
,则图2中的图象对应的函数在下列四式中只可能是( )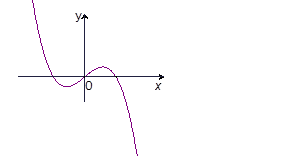
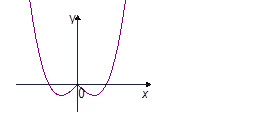
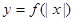
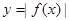
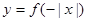
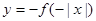
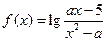 的定义域为
的定义域为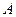 ,若命题
,若命题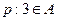 与命题
与命题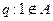 有且仅有一个为真命题,求实数
有且仅有一个为真命题,求实数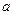 的取值范围。
的取值范围。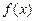 、
、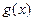 ,如果存在实数
,如果存在实数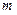 、
、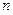 使得
使得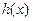 =
=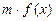 +
+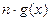 ,则称函数
,则称函数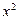 +
+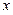 和
和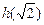 的值;
的值;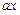 ,
,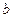
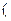
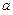 ,
,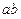 ≠0
≠0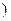 生成,求
生成,求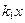 +
+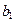 ,
,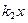 +
+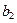
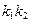 ≠0
≠0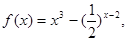 则其零点所在的区间为 ( )
则其零点所在的区间为 ( ) ,已知实数x,y满足|x|≤2,|y|≤2,
,已知实数x,y满足|x|≤2,|y|≤2,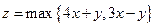 则z的取值范围是 ( )
则z的取值范围是 ( ) 上的函数
上的函数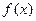 满足
满足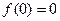 ,
,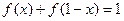 ,且
,且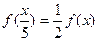 ,当
,当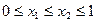 时,有
时,有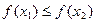 ,求
,求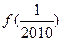 的值
的值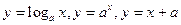 的图像,可能正确的是 ( )
的图像,可能正确的是 ( )