题目内容
【题目】给出下列四个命题:
①f(x)=x3﹣3x2是增函数,无极值.
②f(x)=x3﹣3x2在(﹣∞,2)上没有最大值
③由曲线y=x,y=x2所围成图形的面积是 ![]()
④函数f(x)=lnx+ax存在与直线2x﹣y=0平行的切线,则实数a的取值范围是(﹣∞,2)
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
【答案】A
【解析】解:对于①,∵f′(x)=3x2﹣6x=3x(x﹣2),
当x<0时,f′(x)>0,f(x)是增函数,
当0<x<2时,f′(x)<0,f(x)是减函数,
当x>2时,f′(x)>0,f(x)是增函数;
∴x=0时f(x)有极大值,x=2时f(x)有极小值,∴①错误.
对于②,由①知,当x<0时,f′(x)>0,f(x)是增函数,
当0<x<2时,f′(x)<0,f(x)是减函数;
∴x=0时f(x)有极大值f(0),也是最大值,∴②错误.
对于③,∵ ![]() ,解得
,解得 ![]() ,或
,或 ![]() ;
;
∴由曲线y=x,y=x2所围成图形的面积
S= ![]() (x﹣x2)dx=(
(x﹣x2)dx=( ![]() x2﹣
x2﹣ ![]() x3)
x3) ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,∴③正确.
,∴③正确.
对于④,∵f′(x)= ![]() +a=2(x>0),∴a=2﹣
+a=2(x>0),∴a=2﹣ ![]() <0;
<0;
∴a的取值范围是(﹣∞,2),
又当a=2﹣ ![]() 时,f(x)的一条切线方程为2x﹣y=0,∴④错误.
时,f(x)的一条切线方程为2x﹣y=0,∴④错误.
综上,以上正确的命题为③.
故选:A.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

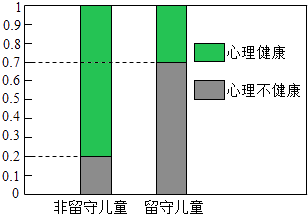
【题目】为研究心理健康与是否是留守儿童的关系,某小学在本校四年级学生中抽取了一个110人的样本,其中留守儿童有40人,非留守儿童有70人,对他们进行了心理测试,并绘制了如图的等高条形图,试问:能否在犯错误的概率不超过0.001的前提下认为心理健康与是否是留守儿童有关系?
参考数据:
P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() (n=a+b+c+d)
(n=a+b+c+d)