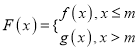Question

【题目】已知函数 ．
（1）求函数f（x）的单调区间；
（2）证明：若a＜5，则对任意 ，有 ．

Answer 1

【答案】
（1）解：f（x）的定义域为（0，+∞），

，

∵a﹣1≥1

当a﹣1＞1时，即a＞2时，f（x）的单调增区间为（0，1），（a﹣1，+∞）；

单调减区间为（1，a﹣1）．

当a﹣1=1时，即a=2时，f（x）的单调增区间为（0，+∞）

（2）要证：对任意 ，

有 ．

不防设x1＞x2，

即证f（x1）﹣f（x2）＞﹣（x1﹣x2）

即证f（x1）+x1＞f（x2）+x2

设 ，x＞0

即证当x1＞x2时，g（x1）＞g（x2）．

即证g（x）在（0，+∞）单调递增．

∵

而△=（a﹣1）2﹣4（a﹣1）=（a﹣1）（a﹣5）

又∵2≤a＜5，

∴△＜0，

∴x2﹣（a﹣1）x+（a﹣1）＞0恒成立，

∴ 对x∈（0，+∞）恒成立，

∴g（x）在（0，+∞）单调递增．

∴原题得证．

【解析】（1）由 ，得当a﹣1＞1时，即a＞2时，f（x）的单调增区间为（0，1），（a﹣1，+∞）；单调减区间为（1，a﹣1）．当a﹣1=1时，即a=2时，f（x）的单调增区间为（0，+∞）（2）要证：对任意 ，有 ．即证f（x1）+x1＞f（x2）+x2设 ，x＞0，即证g（x）在（0，+∞）单调递增．由 ，由g（x）在（0，+∞）单调递增，从而原题得证．
【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减即可以解答此题．