题目内容
已知函数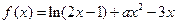 在
在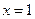 处取得极值.
处取得极值.
(Ⅰ)求函数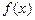 的单调区间;
的单调区间;
(Ⅱ)求证: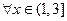 ,
,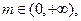
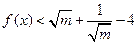 .
.
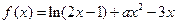 在
在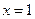 处取得极值.
处取得极值.(Ⅰ)求函数
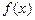 的单调区间;
的单调区间;(Ⅱ)求证:
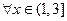 ,
,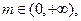
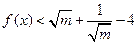 .
.(1)函数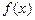 的单调增区间为
的单调增区间为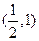 ,
,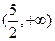 ,单调减区间为
,单调减区间为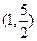 .
.
(2)见解析
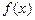 的单调增区间为
的单调增区间为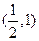 ,
,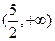 ,单调减区间为
,单调减区间为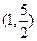 .
.(2)见解析
(Ⅰ)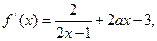
由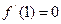 得
得 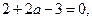
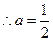 …………………………4分
…………………………4分
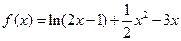 ,
,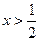
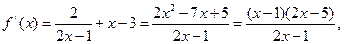
故函数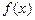 的单调增区间为
的单调增区间为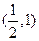 ,
,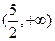 ,单调减区间为
,单调减区间为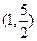 .
.
……………………………………8分
(Ⅱ)由(Ⅰ)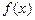 在
在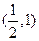 递增,在
递增,在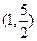 递减,
递减,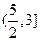 递增,在
递增,在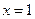 时取极大值
时取极大值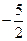
又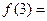
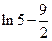 .
. 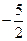
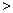
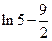
∴在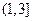 上,
上,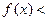
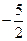 .
.
又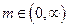 故
故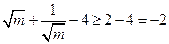 (当且仅当
(当且仅当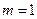 时取等号).
时取等号).
即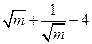 的最小值为
的最小值为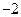 .
.
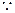
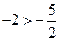
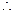
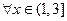 ,
,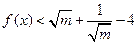 .……………………12分
.……………………12分
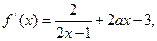
由
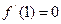 得
得 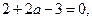
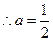 …………………………4分
…………………………4分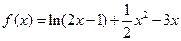 ,
,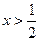
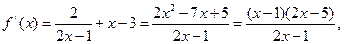
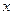 | 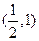 | 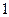 | 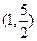 | 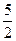 | 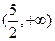 |
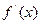 | 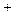 | 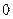 | 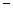 | 0 | 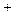 |
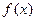 | 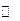 | 极大值 | 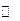 | 极小值 | 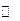 |
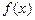 的单调增区间为
的单调增区间为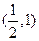 ,
,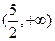 ,单调减区间为
,单调减区间为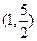 .
.……………………………………8分
(Ⅱ)由(Ⅰ)
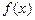 在
在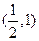 递增,在
递增,在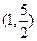 递减,
递减,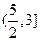 递增,在
递增,在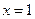 时取极大值
时取极大值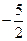
又
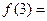
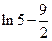 .
. 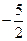
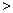
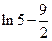
∴在
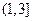 上,
上,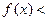
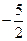 .
.又
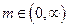 故
故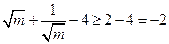 (当且仅当
(当且仅当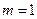 时取等号).
时取等号).即
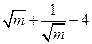 的最小值为
的最小值为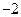 .
.
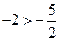
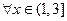 ,
,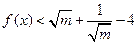 .……………………12分
.……………………12分
练习册系列答案
相关题目
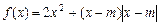 ,
,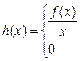
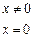 .
.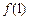 ≥4,求m的取值范围;
≥4,求m的取值范围;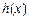 在
在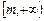 上是单调递增函数;
上是单调递增函数;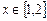 ,不等式
,不等式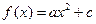 的图象经过点
的图象经过点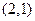 ,且在
,且在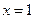 处的切线方程是
处的切线方程是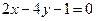
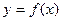 的解析式;
的解析式; 是直线
是直线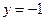 上的动点,自点
上的动点,自点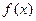 的图象的两条切线
的图象的两条切线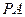 、
、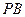 (点
(点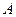 、
、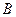 为切点),求证直线
为切点),求证直线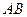 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。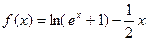 .
.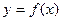 的单调区间,并判断函数的奇偶性;
的单调区间,并判断函数的奇偶性;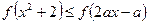 的解集是集合
的解集是集合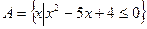 的子集,求实数
的子集,求实数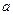 的取值范围.
的取值范围.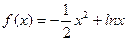 ,
,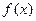 的单调区间;
的单调区间;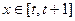
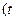 为大于0的常数),求
为大于0的常数),求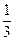 ,1),求函数f(x)的解析式;
,1),求函数f(x)的解析式;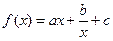 (
(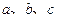 是常数)是奇函数,且满足
是常数)是奇函数,且满足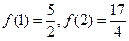 ,
,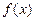 在区间
在区间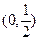 上的单调性并说明理由;
上的单调性并说明理由;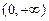 上的最小值.
上的最小值.
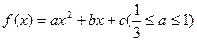 的图象经过A(0,1),且在该点处的切线与直线
的图象经过A(0,1),且在该点处的切线与直线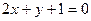 平行.
平行.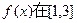 上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.
上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.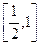 上变化时,证明:
上变化时,证明: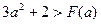
 是偶函数,当
是偶函数,当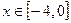 时.
时.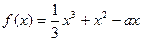 (a为实数).
(a为实数).
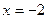 处有极值,求a的值。(6分)
处有极值,求a的值。(6分)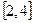 上是减函数,求a的取值范围。(8分)
上是减函数,求a的取值范围。(8分)