题目内容
设a>0,函数f(x)=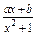 ,b为常数.
,b为常数.
(1)证明:函数f(x)的极大值点和极小值点各有一个;
(2)若函数f(x)的极大值为1,极小值为-1,试求a的值.
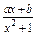 ,b为常数.
,b为常数.(1)证明:函数f(x)的极大值点和极小值点各有一个;
(2)若函数f(x)的极大值为1,极小值为-1,试求a的值.
(1)证明见解析(2)a=2
(1)f′(x)=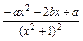 ,
,
令f′(x)=0,得ax2+2bx-a="0 " (*)
∵Δ=4b2+4a2>0,
∴方程(*)有两个不相等的实根,记为x1,x2(x1<x2),
则f′(x)=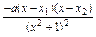 ,
,
当x变化时,f′(x)与f(x)的变化情况如下表:
?可见,f(x)的极大值点和极小值点各有一个.
(2) 由(1)得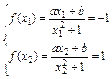
即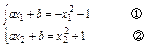
两式相加,得a(x1+x2)+2b=x -x
-x .
.
∵x1+x2=-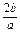 ,∴x
,∴x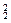 -x
-x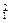 =0,
=0,
即(x2+x1)(x2-x1)=0,
又x1<x2,∴x1+x2=0,从而b=0,
∴a(x2-1)=0,得x1=-1,x2=1,
由②得a=2.
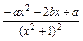 ,
,令f′(x)=0,得ax2+2bx-a="0 " (*)
∵Δ=4b2+4a2>0,
∴方程(*)有两个不相等的实根,记为x1,x2(x1<x2),
则f′(x)=
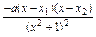 ,
,当x变化时,f′(x)与f(x)的变化情况如下表:
| x | (-∞,x1) | x1 | (x1 ,x2) | x2 | (x2 ,+ ∞) |
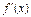 | - | 0 | + | 0 | - |
| f (x) |  | 极小植 |  | 极大值 |  |
(2) 由(1)得
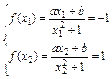
即
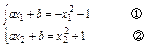
两式相加,得a(x1+x2)+2b=x
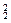 -x
-x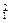 .
.∵x1+x2=-
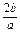 ,∴x
,∴x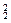 -x
-x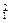 =0,
=0,即(x2+x1)(x2-x1)=0,
又x1<x2,∴x1+x2=0,从而b=0,
∴a(x2-1)=0,得x1=-1,x2=1,
由②得a=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
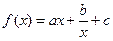 (
(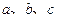 是常数)是奇函数,且满足
是常数)是奇函数,且满足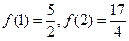 ,
,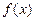 在区间
在区间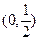 上的单调性并说明理由;
上的单调性并说明理由;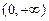 上的最小值.
上的最小值.
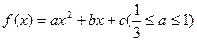 的图象经过A(0,1),且在该点处的切线与直线
的图象经过A(0,1),且在该点处的切线与直线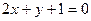 平行.
平行.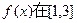 上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.
上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.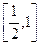 上变化时,证明:
上变化时,证明: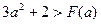
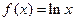 ,
,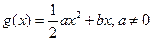 。
。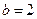 ,且函数
,且函数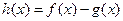 存在单调递减区间,求
存在单调递减区间,求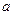 的取值范围;
的取值范围;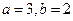 时,求函数
时,求函数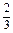 .
.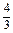 .
.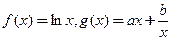 ,它们的图象在
,它们的图象在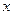 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当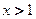 时,
时,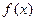 与
与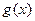 的大小关系是 ( )
的大小关系是 ( )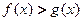
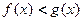

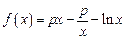 ,
,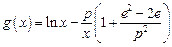 ,其中
,其中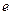 为无理数
为无理数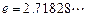 .(1)若
.(1)若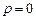 ,求证:
,求证: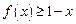 ;(2)若
;(2)若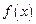 在其定义域内是单调函数,求
在其定义域内是单调函数,求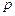 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数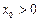 使
使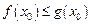 成立?
成立?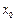 ;否则,说明理由.
;否则,说明理由. 的大致图象,则
的大致图象,则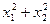 等于( )
等于( )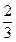
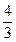
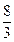
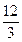
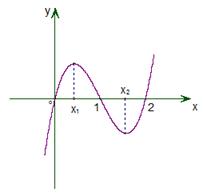

 ,求
,求 .
.