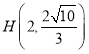题目内容
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(3)记集合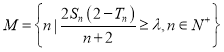 ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)数列![]() 是等差数列,可把已知用
是等差数列,可把已知用![]() 表示出来,列出方程组,解出
表示出来,列出方程组,解出![]() ,从而得到通项公式和胶
,从而得到通项公式和胶![]() 项和
项和![]() ;(2)由已知得
;(2)由已知得![]() ,这是数列前后项的比值,因此可用连乘法求得通项
,这是数列前后项的比值,因此可用连乘法求得通项![]() ,即
,即![]() ,从而有
,从而有![]() ,它可看作是一个等差数列和一个等比数列的乘积,因此其前
,它可看作是一个等差数列和一个等比数列的乘积,因此其前![]() 项和用乘公比错位相减法求得;(3)由(1)(2)求得
项和用乘公比错位相减法求得;(3)由(1)(2)求得![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,只要求得
恒成立,只要求得![]() 的最小值即可,先求出前面几项
的最小值即可,先求出前面几项![]() ,观察归纳猜想出
,观察归纳猜想出![]() 单调性并给出证明(可用
单调性并给出证明(可用![]() 证明数列的单调性),从而可求得最小值,得范围.
证明数列的单调性),从而可求得最小值,得范围.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,由题意得
,由题意得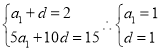
![]()
(2)由题意得![]()
叠乘得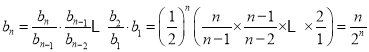
由题意得![]() ①
①
![]() ②
②
②-①得: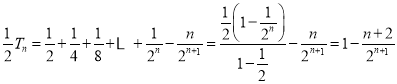
![]()
(3)由上面可得![]() 令
令![]()
则![]()
下面研究数列![]() 的单调性,
的单调性,
![]()
![]() 时,
时,![]() 即
即![]() 单调递减.
单调递减.
所以不等式![]() 解的个数为4,
解的个数为4,![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为![]() .
.
喜欢吃辣 | 不喜欢吃辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由:
下面的临界值表供参考:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: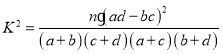 ,其中
,其中![]() )
)