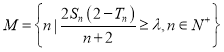Question

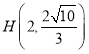【题目】已知椭圆的右焦点为，点在椭圆上.

（1）求椭圆的方程；

（2）点在圆上，且在第一象限，过作的切线交椭圆于两点，问：的周长是否为定值？若是，求出定值；若不是。说明理由.

Answer 1

【答案】（1）；（2）定值为6

【解析】

试题分析：（1）要求椭圆标准方程，就是要确定的值，题中焦点说明，点在椭圆上，把坐标代入标准方程可得的一个方程，联立后结合可解得；（2）定值问题，就是让切线绕圆旋转，求出的周长，为此设直线的方程为（，由它与圆相切可得的关系，，下面来求周长，设，把直线方程与椭圆方程联立方程组，消元后得一元二次方程，可得，由弦长公式得弦长，再求得（这也可由焦半径公式可得），再求周长，可得定值．

试题解析：（1）由题意得

所以椭圆方程为

（2）由题意，设的方程为

与圆相切，，即

由

设，则

又

，同理

（定值）