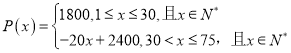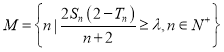题目内容
【题目】若集合![]() 满足
满足![]() ,则称
,则称![]() 为集合
为集合![]() 的一种分拆,并规定:当且仅当
的一种分拆,并规定:当且仅当![]() 时,
时, ![]() 与
与![]() 是集合
是集合![]() 的同一种分拆。若集合
的同一种分拆。若集合![]() 有三个元素,则集合
有三个元素,则集合![]() 的不同分拆种数是 .
的不同分拆种数是 .
【答案】27
【解析】
试题分析:设![]()
①若![]() =时,
=时,![]() =A,此时只有一种分拆.
=A,此时只有一种分拆.
②若![]() 是单元素集时,共有六种分拆,{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}.
是单元素集时,共有六种分拆,{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}.
③若![]() 是双元素集时,共有12种,{1,2}与{3},{1,3},{2,3},{1,2,3};
是双元素集时,共有12种,{1,2}与{3},{1,3},{2,3},{1,2,3};
{1,3}与{2},{1,2},{2,3},{1,2,3};
{2,3}与{1},{1,2},{1,3},{1,2,3};
④若![]() =A={1,2,3},则
=A={1,2,3},则![]() =,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3}共8种.
=,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3}共8种.
综上有1+6+12+8=27

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目