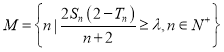题目内容
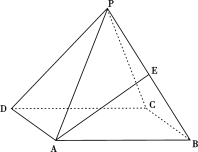
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
(1)求正四棱锥![]() 的外接球半径;
的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求外切球的半径首先确定圆心的位置,进而得到求得半径;(2)容易证明EO∥PD且EO=![]() PD可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求
PD可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求
试题解析:(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,
∴ ∠PAO就是PA与底面ABCD所成的角,∴ tan∠PAO=![]() .
.
又AB=![]() ,则PO=AOtan∠PAO =
,则PO=AOtan∠PAO =![]() .
.
设F为外接球球心,连FA,
易知FA=FP,设FO=x,则
![]()
![]()
(2)连结EO,由于O为BD中点,E为PD中点,所以![]()
![]()
![]() .
.
∴ ![]() 就是异面直线PD与AE所成的角.
就是异面直线PD与AE所成的角.
在Rt![]() 中,
中,![]() .∴
.∴![]() .
.
由![]() ,
,![]() 可知
可知![]() 面
面![]() .所以
.所以![]() ,
,
在Rt![]() 中,
中,![]() ,
,
即异面直线PD与AE所成角的正切值为![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目