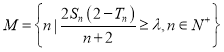题目内容
【题目】已知函数f(x)=xln x.
(1)求函数f(x)的极值点;
(2)设函数g(x)=f(x)-a(x-1),其中a∈R,求函数g(x)在区间[1,e]上的最小值.(其中e为自然对数的底数).
【答案】(1)x=![]() 是函数f(x)的极小值点,极大值点不存在;
是函数f(x)的极小值点,极大值点不存在;
(2)当a≤1时,g(x)的最小值为0;当1<a<2时,g(x)的最小值为a-ea-1;当a≥2时,g(x)的最小值为a+e-ae.
【解析】
试题分析:(1)求导,利用导数的符号变换,研究函数的单调性和极值即可;(2)先通过求导研究函数的单调性,再通过分类讨论法研究![]() 与区间
与区间![]() 的关系求其最值.
的关系求其最值.
试题解析:(1)f′(x)=ln x+1,x>0,由f′(x)=0得x=![]() ,
,
所以f(x)在区间(0,![]() )上单调递减,在区间(
)上单调递减,在区间(![]() ,+∞)上单调递增.
,+∞)上单调递增.
所以,x=![]() 是函数f(x)的极小值点,极大值点不存在.
是函数f(x)的极小值点,极大值点不存在.
(2)g(x)=xln x-a(x-1),则g′(x)=ln x+1-a,由g′(x)=0,得x=ea-1,
所以,在区间(0,ea-1)上,g(x)为递减函数,在区间(ea-1,+∞)上,g(x)为递增函数.
当ea-1≤1,即a≤1时,在区间[1,e]上,g(x)为递增函数,所以g(x)的最小值为g(1)=0.
当1<ea-1<e,即1<a<2时,g(x)的最小值为g(ea-1)=a-ea-1.
当ea-1≥e,即a≥2时,在区间[1,e]上,g(x)为递减函数,所以g(x)的最小值为g(e)=a+e-ae.
综上,当a≤1时,g(x)的最小值为0;当1<a<2时,g(x)的最小值为a-ea-1;当a≥2时,g(x)的最小值为a+e-ae.

练习册系列答案
相关题目