题目内容
11.已知数列{an}满足:a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n}}{{λ}^{n-1}}$=n2+2n(其中常数λ>0,n∈N*).(1)求数列{an}的通项公式;
(2)当λ=4时,若bn=$\frac{{{a_n}-(2n+1)•{r^n}}}{{(n+\frac{1}{2})(1+{r^n})}}$(r∈R,r≠-1),求$\lim_{n→∞}{b_n}$
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,是否存在λ≠1,使得不等式(1-λ)Sn+(2n+1)•λn≤3成立,若存在,求实数λ的取值范围;若不存在,说明理由.
分析 (1)由a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n}}{{λ}^{n-1}}$=n2+2n,得a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n-1}}{{λ}^{n-2}}$=(n-1)2+2(n-1),二者相减,并整理能求出数列{an}的通项公式.
(2)当λ=4时,an=(2n+1)•4n-1,bn=$\frac{2({4}^{n-1}-{r}^{n})}{1+{r}^{n}}$,由此根据r的取值进行分类讨论,能求出$\underset{lim}{n→∞}{b}_{n}$.
(3)${S}_{n}=3+5λ+7{λ}^{2}+…+(2n+1){λ}^{n-1}$,当λ≠1时,利用错位相减法得到(1-λ)Sn=3+$\frac{2λ(1-{λ}^{n-1})}{1-λ}-(2n+1){λ}^{n}$,由此利用反证法能推导出对任意n∈N*,不存在λ≠1,使得不等式(1-λ)Sn+(2n+1)•λn≤3成立.
解答 解:(1)∵数列{an}满足:a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n}}{{λ}^{n-1}}$=n2+2n(其中常数λ>0,n∈N*),
∴a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n}}{{λ}^{n-1}}$=n2+2n,①
a1+$\frac{{a}_{2}}{λ}$+$\frac{{a}_{3}}{{λ}^{2}}$+…+$\frac{{a}_{n-1}}{{λ}^{n-2}}$=(n-1)2+2(n-1),②
①-②,得:$\frac{{a}_{n}}{{λ}^{n-1}}=2n+1$,
∴an=(2n+1)•λn-1.
(2)当λ=4时,an=(2n+1)•4n-1,
bn=$\frac{{{a_n}-(2n+1)•{r^n}}}{{(n+\frac{1}{2})(1+{r^n})}}$=$\frac{(2n+1)•{4}^{n-1}-(2n+1)•{r}^{n}}{(n+\frac{1}{2})(1+{r}^{n})}$=$\frac{(2n+1)({4}^{n-1}-{r}^{n})}{(n+\frac{1}{2})(1+{r}^{n})}$=$\frac{2({4}^{n-1}-{r}^{n})}{1+{r}^{n}}$,
∴当|r|>4时,$\underset{lim}{n→∞}{b}_{n}=-2$,
当|r|<4时,$\underset{lim}{n→∞}{b}_{n}$不存在,
当|r|=4时,$\underset{lim}{n→∞}{b}_{n}$=-$\frac{3}{2}$,
当r=-4时,$\underset{lim}{n→∞}{b}_{n}$不存在.
(3)${S}_{n}=3+5λ+7{λ}^{2}+…+(2n+1){λ}^{n-1}$,
当λ≠1时,${S}_{n}=3+5λ+7{λ}^{2}+…+(2n+1){λ}^{n-1}$,
$λ{S}_{n}=3λ+5{λ}^{2}+…+(2n-1){λ}^{n-1}+(2n+1)$λn,
(1-λ)Sn=3+2(λ+λ2+λ3+…+λn-1)-(2n+1)•λn=3+$\frac{2λ(1-{λ}^{n-1})}{1-λ}-(2n+1){λ}^{n}$,
假设对任意n∈N*,存在λ≠1,使得不等式(1-λ)Sn+(2n+1)•λn≤3成立,
∵$(1-λ){S}_{n}+(2n+1)•{λ}^{n}$=3+$\frac{2λ(1-{λ}^{n-1})}{1-λ}$,
∴(1-λ)Sn+(2n+1)•λn=3+$\frac{2λ(1-{λ}^{n-1})}{1-λ}$≤3,∴$\frac{1-{λ}^{n-1}}{1-λ}≤0$,
但是当0<λ<1时,1-λn-1>0,1-λ>0,∴$\frac{1-{λ}^{n-1}}{1-λ}>0$,n≥2,
当λ>1时,1-λn-1<0,1-λ<0,∴$\frac{1-{λ}^{n-1}}{1-λ}>0,(n≥2)$,矛盾,假设不成立,
∴对任意n∈N*,不存在λ≠1,使得不等式(1-λ)Sn+(2n+1)•λn≤3成立.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的极限的求法,考查满足条件的实数值是否存在的判断与求法,综合性强,难度大,对数学思维的要求较高,解题时要注意错位相减法和反证法的合理运用.

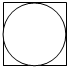 在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )| A. | $\frac{m}{n}$ | B. | $\frac{2m}{n}$ | C. | $\frac{3m}{n}$ | D. | $\frac{4m}{n}$ |
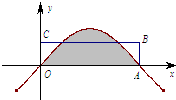 点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )
点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{4}{π}$ |
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
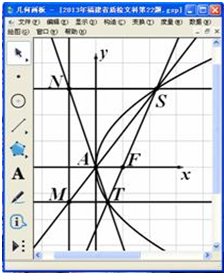 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.