题目内容
已知f(x)=x2+ax+3
(1)当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
(2)当x∈(-∞,1)时,f(x)≥a恒成立,求实数a的取值范围.
(1)当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
(2)当x∈(-∞,1)时,f(x)≥a恒成立,求实数a的取值范围.
(1)∵x2+ax+3-a≥0对任意x∈R恒成立,
∴△=a2-4(3-a)≤0,解得-6≤a≤2,
∴a的范围是{a|-6≤a≤2}.
(2)∵x2+ax+3-a≥0对任意x∈(-∞,1)恒成立,
方法一:设g(x)=x2+ax+3-a,则△≤0或
,
即:a2-4(3-a)≤0或
,
解得:-6≤a≤2或a<-6⇒a≤2.
∴实数a的范围是{a|a≤2}.
方法二:即a≤
对任意x∈(-∞,1)恒成立,
∵1-x>0,
而
=(1-x)+
-2≥2
-2=2,当且仅当x=-1时取等号.
∴实数a的范围是{a|a≤2}.
∴△=a2-4(3-a)≤0,解得-6≤a≤2,
∴a的范围是{a|-6≤a≤2}.
(2)∵x2+ax+3-a≥0对任意x∈(-∞,1)恒成立,
方法一:设g(x)=x2+ax+3-a,则△≤0或
|
即:a2-4(3-a)≤0或
|
解得:-6≤a≤2或a<-6⇒a≤2.
∴实数a的范围是{a|a≤2}.
方法二:即a≤
| x2+3 |
| 1-x |
∵1-x>0,
而
| x2+3 |
| 1-x |
| 4 |
| 1-x |
| 4 |
∴实数a的范围是{a|a≤2}.

练习册系列答案
相关题目
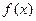 是定义在
是定义在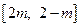 上的奇函数,且对任意
上的奇函数,且对任意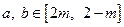 ,当
,当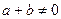 时,都有
时,都有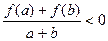 .(Ⅰ)求实数
.(Ⅰ)求实数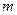 的值;(Ⅱ)解不等式
的值;(Ⅱ)解不等式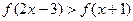 .
.