题目内容
12.(1)设x,y,z∈R,且满足:x2+y2+z2=1,x+2y+3z=√14,求x+y+z的值;(2)设不等式|x-2|<a(a∈N*)的解集为A,且32∈A,12∉A.求函数f(x)=|x+a|+|x-2|的最小值.
分析 (1)14=(x2+y2+z2)(1+4+9)=(x+2y+3z)2,结合柯西不等式,即可求x+y+z的值;
(2)由不等式|x-2|<a的解集为A,求出a=1,把a=1代入函数表达式,即可求出函数f(x)=|x+a|+|x-2|的最小值.
解答 解:(1)由题14=(x2+y2+z2)(1+4+9)=(x+2y+3z)2,
但由柯西不等式,(x2+y2+z2)(1+4+9)≥(x+2y+3z)2,
当且仅当x+2y+3z=√14且x=y2=z3,即{x=√1414y=2√1414z=3√1414时取等,
故取等条件必须成立,此时x+y+z=3√147
(2)因为32∈A,且12∉A,所以|32−2|<a,且|12−2|≥a
解得12<a≤32,
又因为a∈N*,所以a=1
因为|x+1|+|x-2|≥|(x+1)-(x-2)|=3
当且仅当(x+1)(x-2)≤0,即-1≤x≤2时取得等号,
所以f(x)的最小值为3
点评 本题考查柯西不等式,考查求函数的值域问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
17.下面是关于复数z=2−1+i的四个命题:
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中真命题为( )
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |

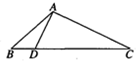 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=