题目内容
18.已知函数f(x)是偶函数,且x≥0时,f(x)=x2-2x+3,试求f(x)在R上的表达式,并画出图象,根据图象写出它的单调区间.分析 设x<0则-x>0,利用已知的解析式和偶函数的性质求出x<0时的解析式,用分段函数的形式表示出来,根据二次函数的图象画出f(x)的图象,由图象求出f(x)的单调区间.
解答 解:设x<0,则-x>0,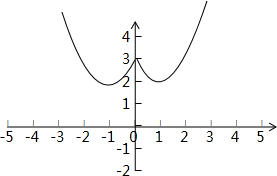
∵x≥0时,f(x)=x2-2x+3,∴f(-x)=x2+2x+3,
∵函数f(x)是偶函数,∴f(x)=f(-x)=x2+2x+3,
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x+3,x≥0}\\{{x}^{2}+2x+3,x<0}\end{array}\right.$,
由二次函数的图象画出此函数的图象:
由图可得:函数f(x)的增区间是(-1,0)、(1,+∞),
减区间是(-∞,-1)、(0,1).
点评 本题考查利用函数的奇偶性求函数的解析式,二次函数的图象,以及分段函数的单调性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.由某个2×2列联表数据计算得随机变量K2的观测值k=6.879,则下列说法正确的是( )
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 两个分类变量之间有很强的相关关系 | |
| B. | 有99%的把握认为两个分类变量没有关系 | |
| C. | 在犯错误的概率不超过1.0%的前提下认为这两个变量间有关系 | |
| D. | 在犯错误的概率不超过0.5%的前提下认为这两个变量间有关系 |