题目内容
7.已知A,B为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右顶点,P为椭圆上异于A,B的任意一点,直线AP,BP分别交椭圆的直线l:x=4于点M,N,则$\overrightarrow{AM}$•$\overrightarrow{BN}$的值为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
分析 由题意作出辅助图象,设点P(2cosθ,$\sqrt{3}$sinθ)(sinθ≠0),M(4,y1),N(4,y2);从而求得$\overrightarrow{AM}$=(6,$\frac{6\sqrt{3}sinθ}{2cosθ+2}$);$\overrightarrow{BN}$=(2,$\frac{2\sqrt{3}sinθ}{2cosθ-2}$);从而解得.
解答 解:由题意作图如下,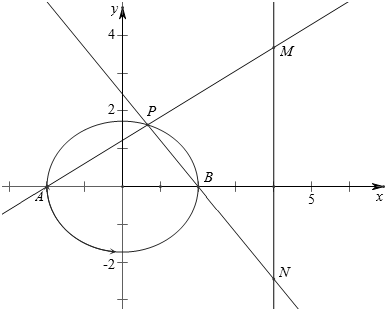
设点P(2cosθ,$\sqrt{3}$sinθ)(sinθ≠0),M(4,y1),N(4,y2);
$\frac{\sqrt{3}sinθ-0}{2cosθ+2}$=$\frac{{y}_{1}-0}{4+2}$,$\frac{\sqrt{3}sinθ-0}{2cosθ-2}$=$\frac{{y}_{2}-0}{4-2}$;
故y1=$\frac{6\sqrt{3}sinθ}{2cosθ+2}$,y2=$\frac{2\sqrt{3}sinθ}{2cosθ-2}$;
$\overrightarrow{AM}$=(6,$\frac{6\sqrt{3}sinθ}{2cosθ+2}$);$\overrightarrow{BN}$=(2,$\frac{2\sqrt{3}sinθ}{2cosθ-2}$);
$\overrightarrow{AM}$•$\overrightarrow{BN}$=12+$\frac{6\sqrt{3}sinθ}{2cosθ+2}$•$\frac{2\sqrt{3}sinθ}{2cosθ-2}$
=12+$\frac{12×3×si{n}^{2}θ}{-4si{n}^{2}θ}$=12-9=3;
故选:B.
点评 本题考查了椭圆的性质的应用及平面向量的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案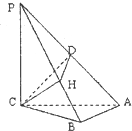 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
| A. | lnx+cosx | B. | lnx-cosx | C. | ex+cosx | D. | ex-cosx |
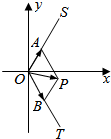 如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.
如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.