题目内容
16.某象棋比赛,规定如下:两名选手比赛时每局胜者得1分,负者得0分,比赛进行到有一人比对方多3分获胜后停止,或打满7局时停止(可以出现没有获胜的情况).设某学校选手甲和选手乙比赛时,甲在每局中获胜的概率为p(p>$\frac{1}{2}$),且各局胜负相互独立.已知第三局比赛结束时比赛停止的概率为$\frac{1}{3}$.甲获胜的概率为$\frac{1400}{2187}$.分析 根据题意,先求出甲每局获胜的概率p,再计算打满3局、打满5局以及打满7局甲获胜的概率,求和即可.
解答 解:比赛进行到第3局结束,应满足甲连胜3局,或乙连胜3局,
则p3+(1-p)3=$\frac{1}{3}$,
化简得,9p2-9p+2=0,
解得p=$\frac{2}{3}$,p=$\frac{1}{3}$(不合题意,舍去);
所以,打满3局甲获胜的概率为${C}_{3}^{3}$•${(\frac{2}{3})}^{3}$=$\frac{8}{27}$,
打满5局甲获胜时,前3局甲2胜第4、5局甲连胜,
其概率为${C}_{3}^{2}$•${(\frac{2}{3})}^{2}$•$\frac{1}{3}$•$\frac{2}{3}$•$\frac{2}{3}$=$\frac{16}{81}$,
打满7局甲获胜时,前5局甲3胜6、7甲连胜,
其概率为${C}_{5}^{3}$•${(\frac{2}{3})}^{3}$•${(\frac{1}{3})}^{2}$•$\frac{2}{3}$•$\frac{2}{3}$=$\frac{320}{729×3}$;
所以,甲获胜的概率为P=$\frac{8}{27}$+$\frac{16}{81}$+$\frac{320}{729×3}$=$\frac{1400}{2187}$.
故答案为:$\frac{1400}{2187}$.
点评 本题考查了相互独立事件的概率计算问题,也考查了一定的计算能力,是综合性题目.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
11.已知直线l的方向向量为$\overrightarrow{a}$=(-1,0,1),点A(1,2,-1)在l上,则点P(2,-1,2)到l的距离为( )
| A. | $\sqrt{15}$ | B. | 4 | C. | $\sqrt{17}$ | D. | 3$\sqrt{2}$ |
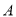 的函数
的函数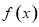 ,若对任意的
,若对任意的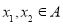 ,有
,有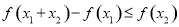 ,则称函数
,则称函数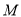 函数”,以下五个函数:①
函数”,以下五个函数:①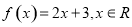 ;②
;② ;③
;③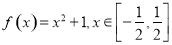 ;④
;④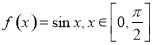 ;⑤
;⑤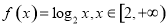 ,其中是“定义上的
,其中是“定义上的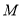 函数”的有( )
函数”的有( )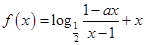 为奇函数,
为奇函数,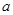 为常数.
为常数.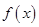 在
在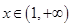 上的单调性,并说明理由;
上的单调性,并说明理由;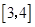 上的每一个
上的每一个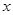 值,不等式
值,不等式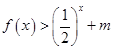 恒成立,求实数
恒成立,求实数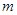 的取值范围.
的取值范围.