Question

4．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{1-（x-1）^{2}}，0≤x＜2}\\{f（x-2），x≥2}\end{array}\right.$，若函数g（x）=f（x）-kx有且仅有四个零点，则实数k的取值范围为（$\frac{\sqrt{6}}{12}$，$\frac{\sqrt{2}}{4}$）．

Answer 1

分析 令h（x）=kx，将函数的零点的个数化为函数交点的个数，作出函数f（x） 的图象，从图象中得到实数k的取值范围即可．

解答 解：令h（x）=kx，
则函数g（x）=f（x）-kx有且只有四个零点可转化为
函数f（x）与h（x）有且只有四个交点；
作出函数f（x） 的图象如下图，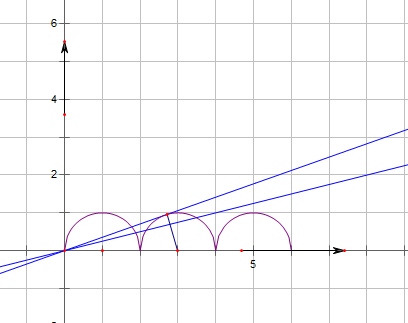

当与第二半圆相切时，有3个交点，此时，k=$\frac{1}{\sqrt{{3}^{2}-1}}$=$\frac{\sqrt{2}}{4}$，
当与第三半圆相切时，有5个交点，此时，k=$\frac{1}{\sqrt{{5}^{2}-1}}$=$\frac{\sqrt{6}}{12}$，
则实数k的取值范围为（$\frac{\sqrt{6}}{12}$，$\frac{\sqrt{2}}{4}$）．
故答案为：（$\frac{\sqrt{6}}{12}$，$\frac{\sqrt{2}}{4}$）．

点评 本题考查了方程的解与函数的零点之间的关系，同时考查了学生的作图能力及数形结合的思想，属于中档题．