题目内容
11.已知直线l的方向向量为$\overrightarrow{a}$=(-1,0,1),点A(1,2,-1)在l上,则点P(2,-1,2)到l的距离为( )| A. | $\sqrt{15}$ | B. | 4 | C. | $\sqrt{17}$ | D. | 3$\sqrt{2}$ |
分析 根据点P到直线l的距离为|$\overrightarrow{PA}$|•sin<$\overrightarrow{a}$,$\overrightarrow{PA}$>,分别计算向量的模长与夹角的正弦值即可.
解答 解:根据题意,得;
$\overrightarrow{PA}$=(-1,3,-3),
$\overrightarrow{a}$=(-1,0,1),
∴cos<$\overrightarrow{a}$,$\overrightarrow{PA}$>=$\frac{1+0-3}{\sqrt{2}×\sqrt{19}}$=-$\sqrt{\frac{2}{19}}$,
∴sin<$\overrightarrow{a}$,$\overrightarrow{PA}$>=$\sqrt{\frac{17}{19}}$;
又∵|$\overrightarrow{PA}$|=$\sqrt{19}$,
∴点P(2,-1,2)到直线l的距离为
|$\overrightarrow{PA}$|sin<$\overrightarrow{a}$,$\overrightarrow{PA}$>=$\sqrt{19}$×$\sqrt{\frac{17}{19}}$=$\sqrt{17}$.
故选:C.
点评 本题考查了空间向量的应用问题,也考查了计算能力的应用问题,是基础题目.

练习册系列答案
相关题目
12.以下是解决数学问题的思维过程的流程

图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )

图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )
| A. | ①-分析法,②-反证法 | B. | ①-分析法,②-综合法 | ||
| C. | ①-综合法,②反证法 | D. | ①-综合法,②-分析法 |
19.已知全集U={0,1,2,3,4},集合A={0,1,3},B={0,1,4},则(∁UA)∪B为( )
| A. | {0,1,2,4} | B. | {0,1,3,4} | C. | {2,4} | D. | {4} |
 ,
,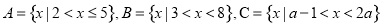 .
. 及
及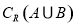 ;
;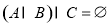 ,求实数
,求实数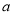 的取值范围.
的取值范围.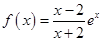 的单调性,并证明当
的单调性,并证明当 时,
时, ;
;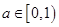 时,函数
时,函数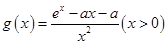 有最小值.设
有最小值.设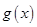 的最小值为
的最小值为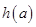 ,求函数
,求函数