题目内容
7.设m为常数,如果函数y=lg(mx2-4x+m-3)的值域为(-∞,+∞),则实数m的取值范围m=0或[-1,4].分析 根据对数函数的定义域得到mx2-4x+m-3能取到(0,+∞)的所有值,所以对m的取值要进行分类讨论:m=0和m≠0两种情况进行解答.
解答 解:∵函数y=lg(mx2-4x+m-3)的值域为(-∞,+∞),
∴mx2-4x+m-3能取到(0,+∞)的所有值:
①当m=0时,y=lg(-4x-3)值域可以为R,符合题意;
②当m>0时,△=16-4m(m-3)≥0,
解得-1≤m≤4,
综上所述,m的取值范围为m=0或[-1,4],
故答案是:m=0或[-1,4].
点评 本题考查了函数的值域.无论用什么方法求函数的值域,都必须考虑函数的定义域.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.已知一元二次方程x2+bx-2c=0,(b,c∈R)有两实根,其中一根x1∈(-1,0),另一根x2∈(0,1),则$\frac{c+1}{b+2}$的取值范围是( )
| A. | ($\frac{1}{4}$,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,1) | D. | (-∞,$\frac{1}{3}$)∪(1,+∞) |
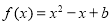 ,且
,且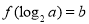 ,
,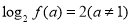 .
.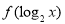 的最小值及对应的
的最小值及对应的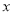 值;
值;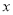 取何值时,
取何值时,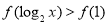 ,且
,且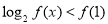 .
.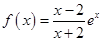 的单调性,并证明当
的单调性,并证明当 时,
时, ;
;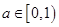 时,函数
时,函数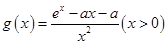 有最小值.设
有最小值.设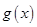 的最小值为
的最小值为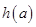 ,求函数
,求函数