Question

【题目】设函数f（x）=x2-4|x|-5．

（Ⅰ）画出y=f（x）的图象；

（Ⅱ）设A={x|f（x）≥7}，求集合A；

（Ⅲ）方程f（x）=k+1有两解，求实数k的取值范围．

Answer 1

【答案】(1)见解析（2）（-∞，-6]∪[6，+∞）(3) {-10}∪（-6，+∞）

【解析】试题分析：

(1)将函数的解析式写成分段函数的形式，然后结合二次函数的性质绘制函数图象即可；

(2)分类讨论和两种情况可得集合A=（-∞，-6]∪[6，+∞）

(3)原问题等价于函数f（x）的图象和直线y=k+1有两个不同的交点，结合直线与二次函数的关于可得实数k的取值范围是{-10}∪（-6，+∞）

试题解析：

（Ⅰ）∵函数f（x）=x2-4|x|-5=，画出y=f（x）的图象，如图：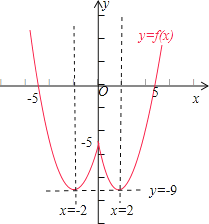

（Ⅱ）由f（x）≥7可得x2-4|x|-5≥7，

即①，或②．

解①得x≥6，解②可得 x≤-6，

故A={x|f（x）≥7}=（-∞，-6]∪[6，+∞）．

（Ⅲ）方程f（x）=k+1有两解，即函数f（x）的图象和直线y=k+1有两个不同的交点，

由于当x=±2时，函数f（x）取得最小值为-9，

结合函数f（x）的图象可得k+1=-9，或 k+1＞-5，

解得k=-10，或k＞-6，

即k的范围为{-10}∪（-6，+∞）．