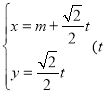题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若![]() 在
在![]() 内为单调增函数,求实数
内为单调增函数,求实数![]() 的取值范围;
的取值范围;
(3)对于![]() ,求证:
,求证: ![]() .
.
【答案】(1)极小值为![]() ,无极大值.(2)
,无极大值.(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)将![]() 代入,对函数求导,由单调性可判断函数的极值;(2)将函数
代入,对函数求导,由单调性可判断函数的极值;(2)将函数 ![]() 在
在![]() 内为单调增函数,则
内为单调增函数,则![]() 在
在![]() 上恒成立,进一步转化为一元二次不等式恒成立问题,可求
上恒成立,进一步转化为一元二次不等式恒成立问题,可求![]() 的取值范围;(3)由函数单调性,当
的取值范围;(3)由函数单调性,当![]() 时,
时, ![]() ,即
,即![]() .令
.令![]() ,变形后可证不等式.
,变形后可证不等式.
试题解析:(1)![]() ,
,
(1)若![]() ,
, ![]() ,令
,令![]() 得
得![]() 或
或![]() (舍去),
(舍去),
令![]() ,所以函数的极小值为
,所以函数的极小值为![]() ,无极大值.
,无极大值.
(2)![]() 在
在![]() 上单调递增,
上单调递增, ![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
当![]() 时,即
时,即![]() 时,
时, ![]() ,所以
,所以![]() ,
,
当![]() 时,即
时,即![]() 时,
时, ![]() ,所以
,所以![]() ,
,
综上![]() .
.
(3)当![]() 时,由(2)知,
时,由(2)知, ![]() 在
在![]() 上单调递增,
上单调递增,
即![]() 时,
时, ![]() ,即
,即![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以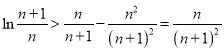 ,
,
所以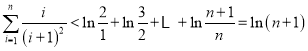 .
.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.