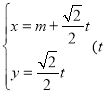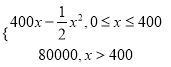题目内容
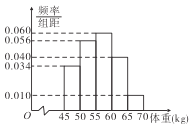
【题目】从某市的高一学生中随机抽取400名同学的体重进行统计，得到如图所示频率分布直方图.
（Ⅰ）估计从该市高一学生中随机抽取一人，体重超过
的概率；
（Ⅱ）假设该市高一学生的体重
服从正态分布
.
（ⅰ）利用（Ⅰ）的结论估计该高一某个学生体重介于
之间的概率；
（ⅱ）从该市高一学生中随机抽取3人，记体重介于
之间的人数为
，利用（ⅰ）的结论，求
的分布列及
.
【答案】（1）
（2）（ⅰ）
（ⅱ）见解析
【解析】试题分析：（1）根据频率分布直方图中小长方形面积等于对应区间概率得体重超过
的频率为
，（2）（ⅰ）
（ⅱ）因为
，所以
.
试题解析：
（Ⅰ）这400名学生中，体重超过
的频率为
，
由此估计从该市高一学生中随机抽取一人，体重超过
的概率为
.
（Ⅱ）（ⅰ）∵
， 
，∴
，
∴
，∴
.
（ⅱ）因为该市高一学生总体很大，所以从该市高一学生中随机抽取3人，可以视为独立重复实验，
其中体重介于
之间的人数
， 
， 
.
所以
的分布列为
|
|
|
|
|
|
|
|
|
|
.
【题目】某公司生产的某种时令商品每件成本为
元，经过市场调研发现，这种商品在未来
天内的日销售量
（件）与时间
（天）的关系如下表所示.
时间 | 1 | 3 | 6 | 10 | 36 | …… |
日销售量
| 94 | 90 | 84 | 76 | 24 | …… |
未来40天内，前20天每天的价格
（元/件）与时间
（天）的函数关系式为 
，且
为整数），后20天每天的价格
（元/件）与时间
（天）的函数关系式为
，且
为整数）.
（Ⅰ）认真分析表格中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据
（件）与 
（天）的关系式；
（Ⅱ）试预测未来 40 天中哪一天的日销售利润最大，最大利润是多少？
（Ⅲ）在实际销售的前 20 天中，该公司决定每销售 1 件商品就捐赠
元利润
给希望工程. 公司通过销售记录发现，前 20 天中，每天扣除捐赠后的日销售利润随时间
（天）的增大而增大，求
的取值范围.
