题目内容
已知函数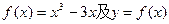 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求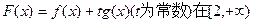 上单调时,t的取值范围.
上单调时,t的取值范围.
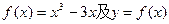 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求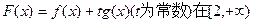 上单调时,t的取值范围.
上单调时,t的取值范围.(Ⅰ) 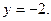 (Ⅱ)
(Ⅱ) 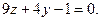 (Ⅲ)
(Ⅲ)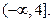
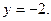 (Ⅱ)
(Ⅱ) 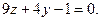 (Ⅲ)
(Ⅲ)
:(Ⅰ)由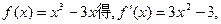 过点P且以P(1,-2)为切点的直线的斜率
过点P且以P(1,-2)为切点的直线的斜率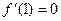 ,
,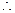 所求直线方程:
所求直线方程: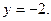 (3分)
(3分)
(Ⅱ)设过P(1,-2)的直线l与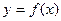 切于另一点
切于另一点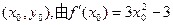
知: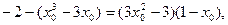 即:
即: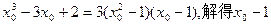
或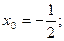 故所求直线的斜率为:
故所求直线的斜率为: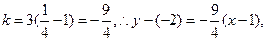
即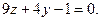 (8分)
(8分)
(Ⅲ)由(Ⅱ)可知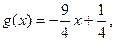 则
则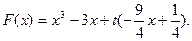
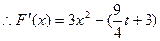
在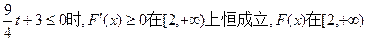 上单调递增, (11分)
上单调递增, (11分)
在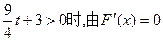 得
得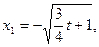
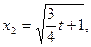 为两极值点,在
为两极值点,在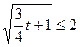 时,
时,
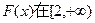 上单调递增,
上单调递增,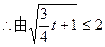
即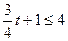
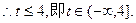 (14分)
(14分)
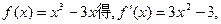 过点P且以P(1,-2)为切点的直线的斜率
过点P且以P(1,-2)为切点的直线的斜率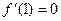 ,
,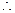 所求直线方程:
所求直线方程: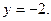 (3分)
(3分)(Ⅱ)设过P(1,-2)的直线l与
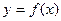 切于另一点
切于另一点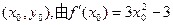
知:
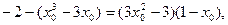 即:
即: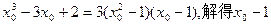
或
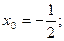 故所求直线的斜率为:
故所求直线的斜率为: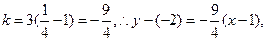
即
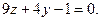 (8分)
(8分)(Ⅲ)由(Ⅱ)可知
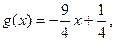 则
则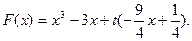
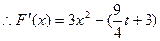
在
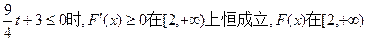 上单调递增, (11分)
上单调递增, (11分)在
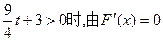 得
得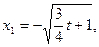
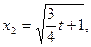 为两极值点,在
为两极值点,在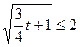 时,
时,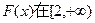 上单调递增,
上单调递增,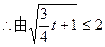
即
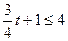
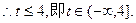 (14分)
(14分)
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
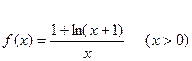 ,
,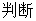
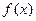 在区间
在区间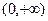 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;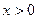 时,
时,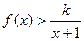 恒成立,求整数
恒成立,求整数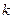 的最小值。
的最小值。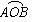 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .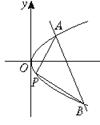
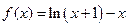 ,(1)求函数
,(1)求函数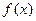 的单调减区间;(2)若
的单调减区间;(2)若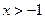 ,证明:
,证明: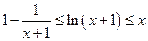 。
。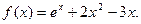 (I)求曲线
(I)求曲线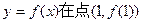 处的切线方程; (Ⅱ)求证函数
处的切线方程; (Ⅱ)求证函数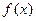 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,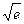 ≈1.6,e0.3≈1.3)
≈1.6,e0.3≈1.3)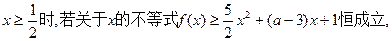 试求实数
试求实数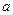 的取值范围。
的取值范围。 为圆心,过另一焦点
为圆心,过另一焦点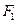 的圆被右准线截的两段弧长之比2:1,
的圆被右准线截的两段弧长之比2:1,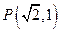 为此平面上一定点,且
为此平面上一定点,且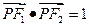 .(1)求椭圆的方程(2)若直线
.(1)求椭圆的方程(2)若直线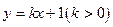 与椭圆交于如图两点A、B,令
与椭圆交于如图两点A、B,令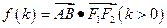 。求函数
。求函数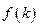 的值域
的值域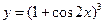 的导数
的导数 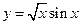 导数为( )
导数为( )



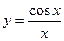 的导数是( )
的导数是( )


