题目内容
已知函数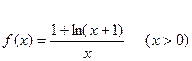 ,
,
(1)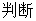
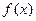 在区间
在区间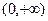 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;
(2)若当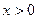 时,
时,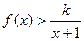 恒成立,求整数
恒成立,求整数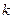 的最小值。
的最小值。
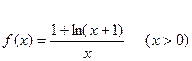 ,
,(1)
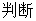
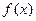 在区间
在区间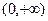 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;(2)若当
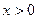 时,
时,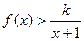 恒成立,求整数
恒成立,求整数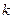 的最小值。
的最小值。(1)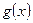 在
在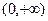 上单调递增;(2)3.
上单调递增;(2)3.
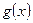 在
在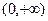 上单调递增;(2)3.
上单调递增;(2)3.(1)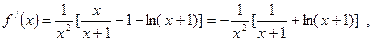 ………2分
………2分
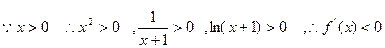 …………3分
…………3分
因此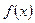 在区间
在区间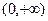 上是减函数. …………4分
上是减函数. …………4分
(2)当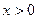 时,
时, 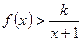 恒成立,即
恒成立,即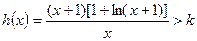 对
对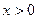 恒成立,即
恒成立,即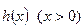 的最小值大于
的最小值大于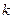 .…………6分
.…………6分
而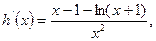 记
记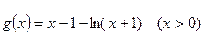 则
则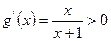
所以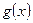 在
在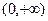 上单调递增. …………9分
上单调递增. …………9分
又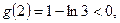
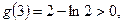
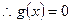 存在唯一实根
存在唯一实根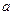 ,且满足
,且满足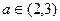 ,
,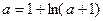 …………11分
…………11分
由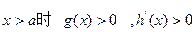 ,
,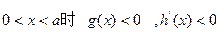 …………12分
…………12分
可知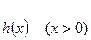 的最小值为
的最小值为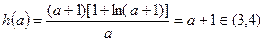 ………13分
………13分
因此正整数 的最大值为3. …………14分
的最大值为3. …………14分
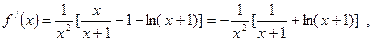 ………2分
………2分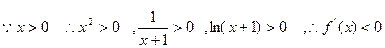 …………3分
…………3分因此
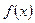 在区间
在区间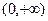 上是减函数. …………4分
上是减函数. …………4分(2)当
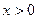 时,
时, 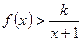 恒成立,即
恒成立,即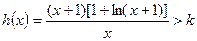 对
对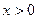 恒成立,即
恒成立,即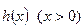 的最小值大于
的最小值大于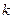 .…………6分
.…………6分而
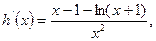 记
记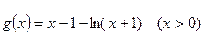 则
则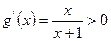
所以
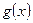 在
在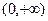 上单调递增. …………9分
上单调递增. …………9分又
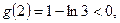
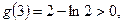
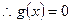 存在唯一实根
存在唯一实根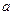 ,且满足
,且满足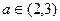 ,
,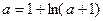 …………11分
…………11分 由
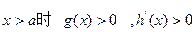 ,
,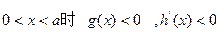 …………12分
…………12分可知
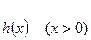 的最小值为
的最小值为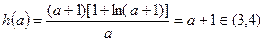 ………13分
………13分因此正整数
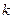 的最大值为3. …………14分
的最大值为3. …………14分
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 (
( ,
,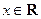 ).
).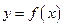 的极值;
的极值; (Ⅱ)若函数
(Ⅱ)若函数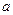 的取值范围.
的取值范围.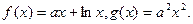
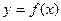 图像上的点到直线
图像上的点到直线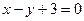 距离的最小值;
距离的最小值;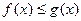 对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由
对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由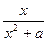 (a
(a >0)在[1,+∞)上的最大值为
>0)在[1,+∞)上的最大值为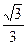 ,求a的值。
,求a的值。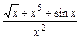 ;
; (1-2cos2
(1-2cos2 );
);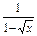 +
+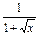 .
.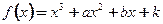 满足
满足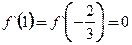 ,
,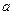 、
、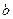 的值及函数
的值及函数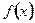 的单调递增区间;
的单调递增区间;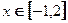 ,不等式
,不等式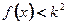 恒成立,求
恒成立,求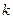 的取值范围。
的取值范围。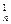 +2C
+2C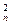 +3C
+3C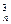 +…+nC
+…+nC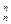 ,(n∈N*)
,(n∈N*)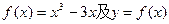 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求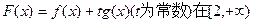 上单调时,t的取值范围.
上单调时,t的取值范围.