题目内容
(本小题满分14分)已知函数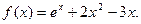 (I)求曲线
(I)求曲线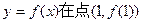 处的切线方程; (Ⅱ)求证函数
处的切线方程; (Ⅱ)求证函数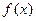 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,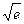 ≈1.6,e0.3≈1.3)
≈1.6,e0.3≈1.3)
(III)当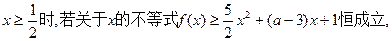 试求实数
试求实数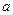 的取值范围。
的取值范围。
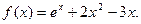 (I)求曲线
(I)求曲线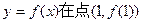 处的切线方程; (Ⅱ)求证函数
处的切线方程; (Ⅱ)求证函数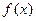 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,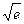 ≈1.6,e0.3≈1.3)
≈1.6,e0.3≈1.3)(III)当
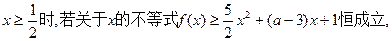 试求实数
试求实数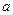 的取值范围。
的取值范围。(I)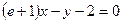 (Ⅱ)
(Ⅱ)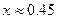 (III)
(III)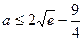
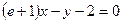 (Ⅱ)
(Ⅱ)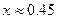 (III)
(III)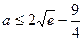
(Ⅰ) ,………1分
,………1分
又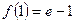 ,
,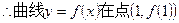 处的切线方程为
处的切线方程为
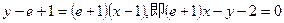 …………3分
…………3分
(Ⅱ)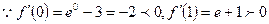 ,
, ………4分
………4分
令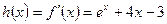 ,则
,则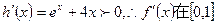 上单调递增,
上单调递增,
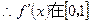 上存在唯一零点,
上存在唯一零点,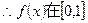 上存在唯一的极值点………6分
上存在唯一的极值点………6分
取区间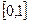 作为起始区间,用二分法逐次计算如下
作为起始区间,用二分法逐次计算如下
由上表可知区间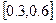 的长度为0.3,所以该区间的中点
的长度为0.3,所以该区间的中点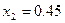 ,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。
,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。
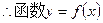 取得极值时,相应
取得极值时,相应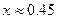 ……9分
……9分
(Ⅲ)由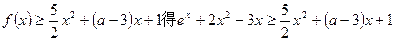 ,
,
即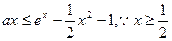 ,
,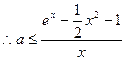 ,……11分
,……11分
令
令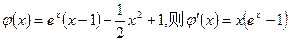
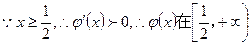 上单调递增,
上单调递增,
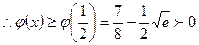 ,因此
,因此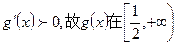 上单调递增,
上单调递增,
则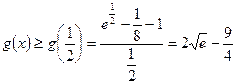 ,
,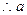 的取值范围是
的取值范围是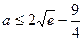 ………14分
………14分
 ,………1分
,………1分又
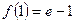 ,
,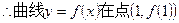 处的切线方程为
处的切线方程为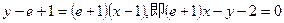 …………3分
…………3分(Ⅱ)
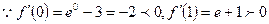 ,
, ………4分
………4分令
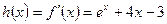 ,则
,则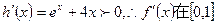 上单调递增,
上单调递增,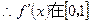 上存在唯一零点,
上存在唯一零点,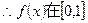 上存在唯一的极值点………6分
上存在唯一的极值点………6分取区间
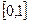 作为起始区间,用二分法逐次计算如下
作为起始区间,用二分法逐次计算如下| 区间中点坐标 | 中点对应导数值 | 取区间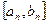 | 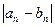 |
| | | 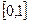 | 1 |
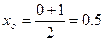 | 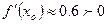 | 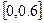 | 0.6 |
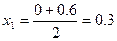 | 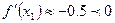 | 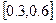 | 0.3 |
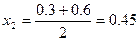 | | | |
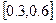 的长度为0.3,所以该区间的中点
的长度为0.3,所以该区间的中点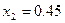 ,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。
,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。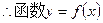 取得极值时,相应
取得极值时,相应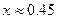 ……9分
……9分(Ⅲ)由
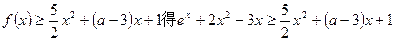 ,
,即
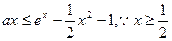 ,
,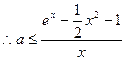 ,……11分
,……11分令

令
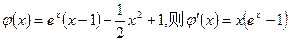
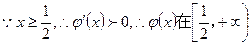 上单调递增,
上单调递增,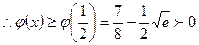 ,因此
,因此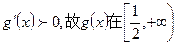 上单调递增,
上单调递增,则
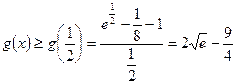 ,
,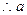 的取值范围是
的取值范围是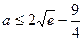 ………14分
………14分
练习册系列答案
相关题目
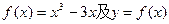 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求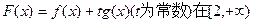 上单调时,t的取值范围.
上单调时,t的取值范围.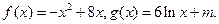 (1)求
(1)求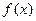 在区间
在区间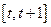 上的最大值
上的最大值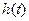 ; (2)若方程
; (2)若方程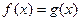 有且只有三个不同的实根,求实数
有且只有三个不同的实根,求实数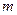 的取值范围.
的取值范围.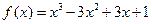 的反函数是
的反函数是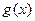 ,则
,则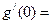 ___________.
___________.
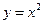 (
(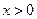 )与函数
)与函数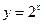 的图像所围成的封闭区域的面积.
的图像所围成的封闭区域的面积.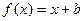 的图像与函数
的图像与函数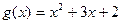 的图象相切,记
的图象相切,记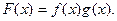
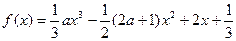 ,
,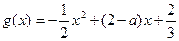
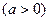 (Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,
(Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,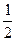 ]内至少存在一实数
]内至少存在一实数 x0使得
x0使得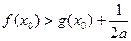 成立,求实数a的取值范围.
成立,求实数a的取值范围.