题目内容
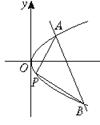
已知直线x+2y-4=0与抛物线y2=4x相交于A、B两点,O是坐标原点,P是抛物线的弧 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .
 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .
P(4,-4)
|AB|为定值,△PAB面积最大,只要P到AB的距离最大,只要点P是抛物线的平行于AB的切线的切点,设P(x,y).由图可知,点P在x轴下方的图象上
∴y=-2
 ,∴y′=-
,∴y′=-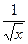 ,∵kAB=-
,∵kAB=- ,∴-
,∴-
∴x=4,代入y2=4x(y<0)得y=-4. ∴P(4,-4)

练习册系列答案
相关题目
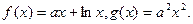
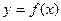 图像上的点到直线
图像上的点到直线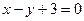 距离的最小值;
距离的最小值;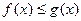 对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由
对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由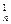 +2C
+2C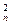 +3C
+3C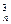 +…+nC
+…+nC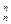 ,(n∈N*)
,(n∈N*)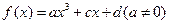 是
是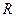 上的奇函数,当
上的奇函数,当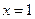 时
时 取得极值
取得极值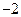 .
.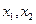
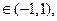 不等式
不等式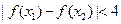 恒成立.
恒成立.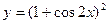 ,则
,则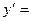 .
.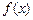 满足
满足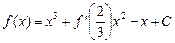 (其中
(其中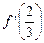 为
为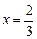 处的导数,
处的导数,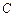 为常数).(1)求函数
为常数).(1)求函数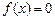 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数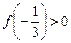 ,求函数
,求函数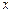 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.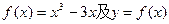 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求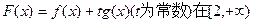 上单调时,t的取值范围.
上单调时,t的取值范围.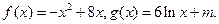 (1)求
(1)求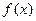 在区间
在区间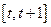 上的最大值
上的最大值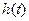 ; (2)若方程
; (2)若方程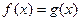 有且只有三个不同的实根,求实数
有且只有三个不同的实根,求实数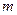 的取值范围.
的取值范围.