题目内容
已知函数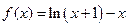 ,(1)求函数
,(1)求函数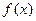 的单调减区间;(2)若
的单调减区间;(2)若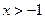 ,证明:
,证明: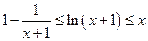 。
。
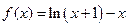 ,(1)求函数
,(1)求函数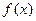 的单调减区间;(2)若
的单调减区间;(2)若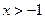 ,证明:
,证明: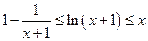 。
。证明略
(1)函数的定义域为 ,
, ,由
,由 及
及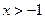 得
得 ,∴当
,∴当 时,
时,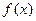 是减函数。即函数的单调减区间是
是减函数。即函数的单调减区间是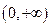 。(2)由(1)知,当
。(2)由(1)知,当 时,
时, ,当
,当 时,
时, ,因此当
,因此当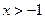 时,
时,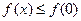 ,即
,即 ,∴
,∴ ,令
,令 ,即
,即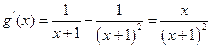 ,∴当
,∴当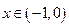 时,
时, ,当
,当 时,
时,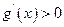 ,∴当
,∴当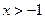 时,
时,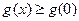 ,即
,即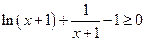 ∴
∴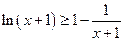 ,综上所述,当
,综上所述,当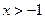 时,有
时,有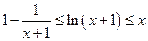 。
。
 ,
, ,由
,由 及
及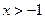 得
得 ,∴当
,∴当 时,
时,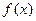 是减函数。即函数的单调减区间是
是减函数。即函数的单调减区间是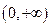 。(2)由(1)知,当
。(2)由(1)知,当 时,
时, ,当
,当 时,
时, ,因此当
,因此当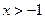 时,
时,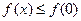 ,即
,即 ,∴
,∴ ,令
,令 ,即
,即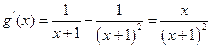 ,∴当
,∴当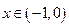 时,
时, ,当
,当 时,
时,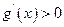 ,∴当
,∴当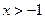 时,
时,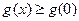 ,即
,即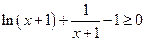 ∴
∴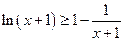 ,综上所述,当
,综上所述,当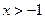 时,有
时,有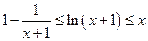 。
。
练习册系列答案
相关题目
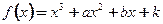 满足
满足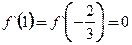 ,
,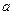 、
、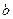 的值及函数
的值及函数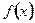 的单调递增区间;
的单调递增区间;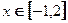 ,不等式
,不等式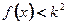 恒成立,求
恒成立,求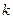 的取值范围。
的取值范围。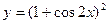 ,则
,则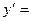 .
.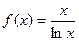 .(Ⅰ)求函数
.(Ⅰ)求函数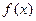 的单调减区间和极值;(Ⅱ)当
的单调减区间和极值;(Ⅱ)当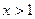 时,若
时,若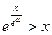 恒成立,求实数
恒成立,求实数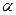 的取值范围.
的取值范围.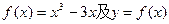 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求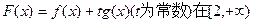 上单调时,t的取值范围.
上单调时,t的取值范围.
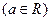 ,
,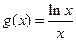 ,其中
,其中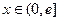 (1)若
(1)若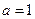 ,求
,求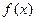 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明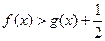 ;(3)是否存在实数
;(3)是否存在实数 ,使
,使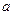 的值,若不存在,说明理由.
的值,若不存在,说明理由.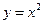 (
(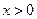 )与函数
)与函数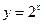 的图像所围成的封闭区域的面积.
的图像所围成的封闭区域的面积. 的导数为( )
的导数为( )



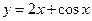 ,则
,则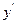 等于( )
等于( )


