题目内容
已知函数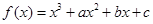 在
在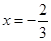 与
与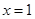 时都取得极值.
时都取得极值.
(1)求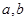 的值;
的值;
(2)若对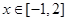 ,不等式
,不等式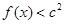 恒成立,求
恒成立,求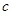 的取值范围.
的取值范围.
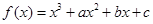 在
在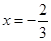 与
与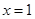 时都取得极值.
时都取得极值.(1)求
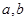 的值;
的值;(2)若对
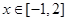 ,不等式
,不等式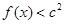 恒成立,求
恒成立,求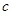 的取值范围.
的取值范围.(1)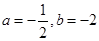 ;(2)
;(2)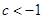 或
或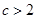 .
.
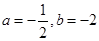 ;(2)
;(2)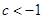 或
或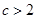 .
.试题分析:(1)先求出
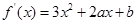 ,进而得到
,进而得到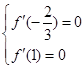 ,从中解方程组即可得到
,从中解方程组即可得到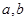 的值,解出
的值,解出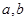 的值后,要注意检验是否符合要求;(2)要使对
的值后,要注意检验是否符合要求;(2)要使对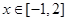 ,不等式
,不等式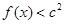 恒成立问题,则只需
恒成立问题,则只需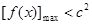 ,从而目标转向函数
,从而目标转向函数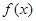 的最大值,根据(1)中所得的
的最大值,根据(1)中所得的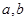 值,确定函数
值,确定函数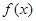 在区间
在区间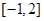 的最大值,进而求解不等式
的最大值,进而求解不等式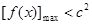 即可.
即可.试题解析:(1)因为
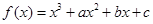 ,所以
,所以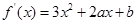
由
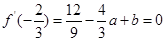 ,
,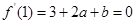 得
得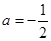 ,
,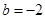
当
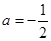 ,
,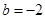 时,所以
时,所以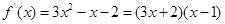 ,列表如下
,列表如下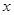 | 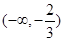 | 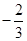 | 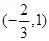 | 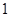 | 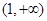 |
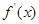 | 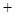 | 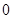 | 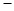 | 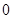 | 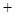 |
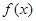 |  | 极大值 |  | 极小值 |  |
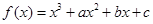 在
在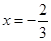 与
与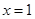 时都取得极值的要求,所以
时都取得极值的要求,所以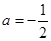 ,
,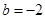
(2)
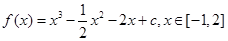
由(1)可知
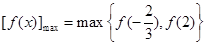
当
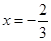 时,
时,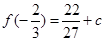 为极大值,而
为极大值,而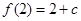
所以
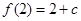 为最大值,要使
为最大值,要使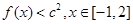 恒成立,则只需
恒成立,则只需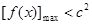 即
即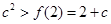 ,解得
,解得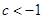 或
或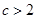 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
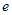 是自然对数的底数,函数
是自然对数的底数,函数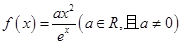 。
。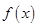 的单调递增区间;
的单调递增区间;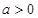 时,函数
时,函数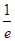 ,求
,求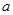 的值。
的值。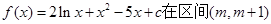 上为递减函数,则m的取值范围是 。
上为递减函数,则m的取值范围是 。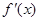 是
是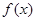 的导函数,
的导函数,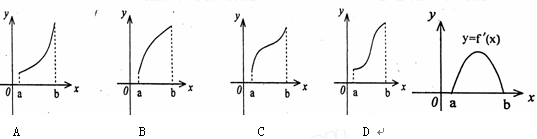
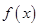 在R上可导,其导函数
在R上可导,其导函数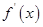 ,且函数
,且函数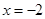 处取得极小值,则函数
处取得极小值,则函数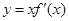 的图像可能是( )
的图像可能是( )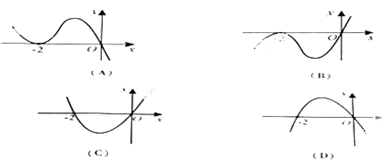
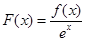 是定义在
是定义在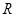 上的函数,其中
上的函数,其中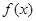 的导函数为
的导函数为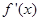 ,满足
,满足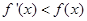 对于
对于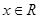 恒成立,则
恒成立,则



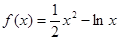 的单调递减区间为( )
的单调递减区间为( ) 1,1)
1,1)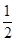 x2+blnx在区间[
x2+blnx在区间[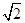 ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.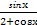 的单调递增区间是 .
的单调递增区间是 .