题目内容
11.已知函数f(x)=x2+bx+c(b,c∈R)(1)方程f(x)-x=0的两根满足0<x1<x2<1,证明:当0<x<x1时,x<f(x)<x1;
(2)对于满足c≥|b|的任意实数b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
分析 (1)由题意可得f(x1)=x1,f(x)在(0,x1)上是减函数,而y=x在(0,x1)上是增函数,数形结合可得要证的不等式成立.
(2)当c>|b|时,M≥$\frac{c+2b}{c+b}$,令$\frac{b}{c}$=t,则-1<t<1,令g(t)=$\frac{c+2b}{c+b}$,求得g(t)的值域,可得M≥$\frac{3}{2}$.当c=|b|时,M=$\frac{3}{2}$检验满足条件,综合可得结论.
解答 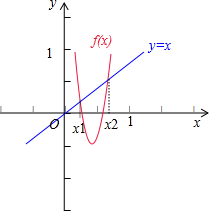 解:(1)证明:∵f(x)=x2+bx+c,方程f(x)-x=0的两根满足0<x1<x2<1,
解:(1)证明:∵f(x)=x2+bx+c,方程f(x)-x=0的两根满足0<x1<x2<1,
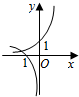
∴f(x1)=x1,f(x)在(0,x1)上是减函数,而y=x在(0,x1)上是增函数,如图所示:
故当0<x<x1时,x<f(x)<f(x1)=x1,即 x<f(x)<x1成立.
(2)由于c≥|b|,不等式f(c)-f(b)≤M(c2-b2)恒成立,
∴当c>|b|时,M≥$\frac{f(c)-f(b)}{{c}^{2}{-b}^{2}}$=$\frac{c+2b}{c+b}$.
令$\frac{b}{c}$=t,则-1<t<1,令g(t)=$\frac{c+2b}{c+b}$=2-$\frac{1}{t+1}$,则g(t)的值域为(-∞,$\frac{3}{2}$),
∴M≥$\frac{3}{2}$.
当c=|b|时,由于f(x)的对称轴为x=-$\frac{b}{2}$,f(0)=c=f(-b),可得c=-b=f(-b),
再结合(1),可得c=-b=2,此时,f(x)=x2 -2x+2=(x-1)2+1,f(c)=f(2)=2,
f(b)=f(-2)=10,f(c)-f(b)=-8,显然f(c)-f(b)≤$\frac{3}{2}$(c2-b2)恒成立,
综上可得,M的最小值为$\frac{3}{2}$.
点评 本题主要考查二次函数的性质,一元二次方程根与系数的关系,体现了转化、分类讨论的数学思想,属于中档题.

| A. | {x|x<-1或x>4} | B. | {x|x≤-1或x≥4} | C. | {x|-1<x<4} | D. | {x|-1≤x≤4} |
| A. | -$\sqrt{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
| A. | $-\sqrt{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |