题目内容
19．复数z=（a2-2a-3）+（|a-2|-1）i不是纯虚数，则实数a的取值范围是（-∞，-1）∪（-1，+∞）．分析 若复数z=（a2-2a-3）+（|a-2|-1）i是纯虚数，则a2-2a-3=0，|a-2|-1≠0，解得a=-1，利用补集的定义即可得出答案．
解答 解：若复数z=（a2-2a-3）+（|a-2|-1）i是纯虚数，
则a2-2a-3=0，|a-2|-1≠0，
解得a=-1，
∴当a≠-1时，复数z=（a2-2a-3）+（|a-2|-1）i不是纯虚数，
故答案为：（-∞，-1）∪（-1，+∞）．
点评 本题考查了纯虚数的定义、补集的意义，考查了计算能力，属于基础题．
练习册系列答案
相关题目
9．已知O为△ABC的外心，满足$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow 0$，则△ABC的最大内角的余弦值为（ ）
| A． | $-\frac{{\sqrt{10}}}{10}$ | B． | $\frac{{\sqrt{10}}}{10}$ | C． | $-\frac{{\sqrt{5}}}{5}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
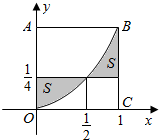在如图的正方形OABC内任取一点，此点在由曲线y=x2和直线x=0，x=1，y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$．