题目内容
20.已知a∈R,复数z=$\frac{n-i}{1-i}$是纯虚数(i是虚数单位),则a=( )| A. | -$\sqrt{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
分析 化简复数z,并且按照纯虚数的定义列出方程组,求出a的值.
解答 解:∵$z=\frac{{({a-i})({1+i})}}{{({1-i})({1+i})}}=\frac{a+1}{2}+\frac{a-1}{2}i$,
由题意,得$\frac{a+1}{2}=0$且$\frac{a-1}{2}≠0$,
∴a=-1.
故选:B.
点评 本题考查了复数的代数运算与纯虚数的概念,是基础题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
5.奇函数f(x)满足f(x+2)=-f(x),当x∈(0,1)时,f(x)=3x+$\frac{1}{2}$,则f(log354)=( )
| A. | -2 | B. | -$\frac{7}{6}$ | C. | $\frac{7}{6}$ | D. | 2 |
12.已知R为实数集,集合A={x|x2≥4},B={y|y=|tanx|},则(∁RA)∩B=( )
| A. | {x|x≤2} | B. | {x|x>0} | C. | {x|0≤x<2} | D. | {x|0<x<2} |
10.某商场以每件30元的价格购进一种玩具.通过试销售发现,逐渐提高售价,每天的利润增大,当售价提高到45元时,每天的利润达到最大值为450元,再提高售价时,由于销售量逐渐减少利润下降,当售价提高到60元时,每天一件也卖不出去.设售价为x,利润y是x的二次函数,则这个二次函数的解析式是( )
| A. | y=-2(x-30)(x-60) | B. | y=-2(x-30)(x-45) | C. | y=(x-45)2+450 | D. | y=-2(x-30)2+450 |
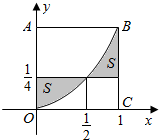 在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.